Le reti neurali feed-forward sono composte da due o più strati di neuroni interconnessi ove l’orientamento dei segnali in entrata segue una e una sola direzione dall’ingresso fino all’uscita, pertanto neuroni dello stesso livello non hanno interconnessioni.
Questa architettura è una delle più diffuse ed utilizzate in assoluto. Negli anni ottanta è stata introdotta [5] la prima versione dell’algoritmo di addestramento “Error Backpropagation”. Con questo metodo, grazie ad una brillante soluzione, fu finalmente possibile addestrare reti più complesse (con due o più strati) del perceptron semplice. In questi casi, quando la rete possiede due o più strati, si parla di “Multi-layers perceptron”.
Tramite il processo di apprendimento, la rete neurale (d’ora in poi “ANN”, Artificial Neural Network) viene preparata a lavorare con certe classi di input, o meglio, funge da classificatore di pattern. Dal punto di vista matematico la rete cerca di approssimare una certa funzione per la soluzione di un dato problema. Dal punto di vista biologico rappresentano invece una analogia con le reti neurali celebrali. Le ANNs si ispirano ad esse, riproducendo, seppur in maniera semplificata, i principi di funzionamento e di apprendimento delle reti biologiche.
In questo articolo non si cercherà di farne una adeguata introduzione, che richiederebbe molto tempo e molto spazio, vedremo invece, prima le basi teoriche dell’algoritmo di apprendimento Error Backpropagation (d’ora in poi BACKPROP) e, successivamente, alcune delle sue molte varianti più recenti.
Data l’abbondanza di materiale circa la teoria matematica di questi modelli e algoritmi e alla penuria di spiegazioni sui metodi numerici, affronteremo a grandi linee anche l’applicazione pratica servendoci di linguaggio C++.
Normalmente di distinguono due fasi di esecuzione: l’apprendimento ed il funzionamento. Ci concentreremo sul primo, il più complesso da affrontare. L’addestramento prevede la presentazione ripetuta di un set di vettori di input assieme ad un set di vettori di output e l’esecuzione dell’algoritmo di addestramento (epoca). Tramite BACKPROP la rete neurale crea una corrispondenza tra questi due vettori. In altre parole, i valori delle connessioni fra neuroni rappresenta una matrice di correlazione fra i due vettori.
Schematizzando una rete MLP a 3 strati, per ogni input presentato, si sviluppa la seguente dinamica:
Partendo dai neuroni dello strato di input, viene calcolato il potenziale ‘P’ pari alla somma pesata degli output dei suoi neuroni in entrata. L’output del neurone è funzione del suo potenziale. In molti casi si utilizza una funzione sigmoidale per il trasferimento, che mantiene l’output del neurone entro il range 0 – 1.
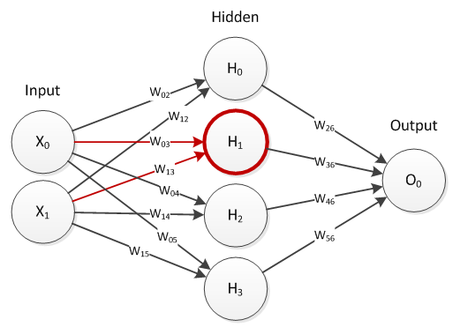
Figura 1: Rete Feed-forward, potenziale neurone nascosto.
Generalizzando in formule, il potenziale ‘P’ è dato da:
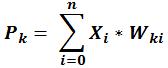
Dove ‘X’ è il i-esimo valore in input, ‘W’ il peso sinaptico che collega il neurone k-esimo con l’i-esimo, n sono il numero di input.
Es. Per il neurone H1 si ha quindi:
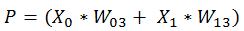
Come abbiamo detto, il valore di output di ogni neurone è determinato da una funzione :
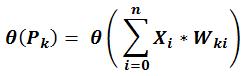
Partendo dagli ingressi e continuando fino all’uscita, determinare il valore di output della rete è semplice. In questo caso, espandendo le equazioni generali si ottiene per l’unico neurone di output:
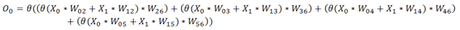
La determinazione dei corretti valori dei pesi ‘W’ della rete in modo che per ogni vettore di input a anche per qualsiasi altro vettore di input simile a quelli utilizzati per l’addestramento, vi sia un vettore di output che rappresenta una certa classe, è compito dell’algoritmo di addestramento.
Come viene spiegato molto bene in [3], per la formulazione dell’algoritmo di addestramento BACKPROP, basato sulla regola di Hebb [6], si parte dalle equazioni degli errori della rete, (Errore quadratico medio) che vengono calcolate dai neuroni di uscita. L’errore generale della rete è determinato da:
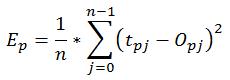
Dove ‘Ep’ è l’errore per il pattern p-esimo presentato alla rete, n è il numero di neuroni dello strato nascosto, ‘O’ è l’output del j-esimo neurone e ‘t’ è il j-esimo valore target del vettore di output del pattern p-esimo.
La sommatoria degli errori dei vari pattern costituisce l’errore sull’intero set:
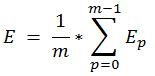
Dove ‘m’ è il numero dei pattern del set.
In analisi numerica, il concetto di derivata ricopre un ruolo fondamentale quando è necessario ottimizzare una funzione. Infatti, come è dimostrato in [3] e [5] BACKPROP calcola la variazione dei pesi sinaptici della rete calcolando la derivata della funzione di errore rispetto al peso di cui calcolare la variazione.

Dove Oi corrisponde al valore di output del neurone precedente, f’() è la derivata del valore di uscita del neurone j-esimo. In particolare l’equazione che descrive l’errore per il neurone j-esimo corrisponde a:
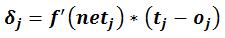
Unendo questa formula alla precedente si ottiene:
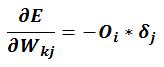
Queste ultime due eq. si utilizzano per calcolare l’errore dei neuroni dello strato di uscita. Sino al 1986 non si sapeva come calcolare il valore di errore degli strati nascosti, quindi era impossibile calcolarne la variazione dei pesi delle connessioni. A metà degli anni ottanta si trovò una brillante soluzione al problema, si pensò di propagare all’indietro l’errore calcolato sullo strato di uscita, è come se la rete venisse eseguita partendo dalle sue uscite. Quindi l’errore dei neuroni nascosti corrisponde alla sommatoria degli errori dei neuroni dello strato successivo moltiplicato il valore dei rispettivi pesi sinaptici. Schematizzando, l’errore dei neuroni nascosti si calcola quindi nel modo seguente:
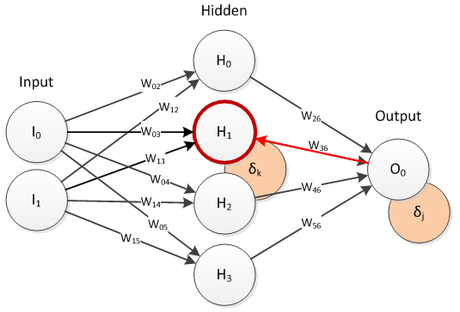
Figura 2: Rete feed-forward, retroazione dell’errore.
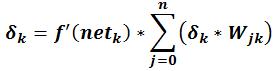
Quando è stato calcolato l’errore e la derivata per ogni neurone della rete, si passa all’aggiornamento dei pesi di tutte le sue connessioni.
Per il calcolo della variazione di ogni singolo peso, BACKPROP utilizza un coefficiente di apprendimento che influisce su velocità di apprendimento e precisione finale della rete.
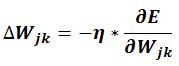
Il learning rate è un valore compreso fra 0.1 e 1. Il suo valore è determinante nella riuscita dell’addestramento e sulla velocità dell’intero processo.
Una volta calcolata la variazione, si passa all’aggiornamento dei pesi sinaptici:
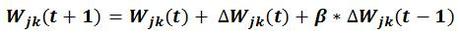
Il coefficiente beta è il ‘momentum’. Un coefficiente che moltiplicato all’aggiornamento eseguito nella iterazione precedente facilita il processo di apprendimento. [3]
L’implementazione di BACKPROP e di altri algoritmi e configurazioni di ANNs li ho implementarli in una libreria di classi C++. Ne vedremo alcune parti inerenti all’algoritmo BACKPROP.
Nella libreria ho utilizzato uno stile fortemente OO in modo che il codice risulti leggibili con poco sforzo. Come è evidente, esso è “parlante” e riduce la quantità di commenti necessari migliorandone la leggibilità e la comprensione. Quella che segue è la routine di addestramento generale di BACKPROP e le sue varianti, in qui vengono calcolati gli errori di tutti i neuroni della rete partendo dall’output e propagando tali valori all’indietro.
// [...]
#pragma region PropagationBase
void PropagationBase::Training(bool OnLine)
{
// Training local variables
double pErr; // Error over the single pattern
double eErr = 0; // Error over the entire epoch
uint epoch = 0; // Epochs counter
// Initialization
// Reset network memory by synapses randomization
network->Reset();
for(;;)
{
for(uint i = 0; i < set->size(); i++)
{
// Set 'i'th input pattern
network->SetInput(set->GetPatternAt(i)->GetDataInput());
// Execution
network->Exec();
// Update error on pattern 'i' (mean square error on pattern)
pErr = 0;
for(uint j = 0; j < network->GetOutputNeurons()->size(); j++)
{
pErr += pow(set->GetPatternAt(i)->GetDataOutput()[j] - network->GetOutputNeuronAt(j)->Output(), 2);
}
pErr *= (1.0/(double)network->GetOutputNeurons()->size());
// Update error over the entire epoch
eErr += pErr;
/* Compute derivatives for all connections of the network */
// Compute delta for the neurons of output layer
for(uint o = 0; o < network->GetOutputNeurons()->size(); o++)
{
network->GetOutputNeuronAt(o)->SetDelta(
network->GetOutputNeuronAt(o)->Derivative() * (set->GetPatternAt(i)->GetDataOutput()[o] - network->GetOutputNeuronAt(o)->Output())
);
// Compute derivatives for each synapse of the layer
for(uint s = 0; s < network->GetOutLayer()->GetNeuronAt(o)->GetInSyn()->size(); s++)
{
network->GetOutLayer()->GetNeuronAt(o)->GetSynapseAt(s)->ComputeDerivative(network->GetOutLayer()->GetNeuronAt(o)->GetDelta());
}
}
for(int h = network->GetHiddenLayers()->size() - 1; h >= 0; h--)
{
// Back prop the error
for(uint n = 0; n < network->GetHiddenLayerAt(h)->GetNeurons()->size(); n++)
{
if(!network->GetHiddenLayerAt(h)->GetNeuronAt(n)->IsBiasNeuron())
{
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->AcquiringDeltaError();
}
}
// Compute delta for hidden layers and their neurons
for(uint n = 0; n < network->GetHiddenLayerAt(h)->GetNeurons()->size(); n++)
{
if(!network->GetHiddenLayerAt(h)->GetNeuronAt(n)->IsBiasNeuron())
{
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->SetDelta(
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetError() * network->GetHiddenLayerAt(h)->GetNeuronAt(n)->Derivative()
);
// Compute derivatives for each synapse of the layer
for(uint s = 0; s < network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetInSyn()->size(); s++)
{
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetSynapseAt(s)->ComputeDerivative(network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetDelta());
}
}
}
}
if(OnLine)
{
OnLineLearning();
Adjust();
}
else
BatchLearning();
}
// Compute and checks the error of the network (mse)
eErr *= (1.0/(double)set->size()); // Mean square error over the entire trainig set
if(eErr <= ErrorTarget)
return; // Training end, target error has been reached
// Add network error to debug vector
_DEBUG_net_error_v.push_back(eErr);
// Batch
if(!OnLine)
{
// Update the weights
Adjust();
// Clean after update
cleanUpdateWeights();
}
// Check number of epochs
if(max_epochs <= ++epoch)
return;
// else continue training
eErr = 0;
}
}
// [...]
// [...]
void synapse::ComputeDerivative(double neuron_delta)
{
last_derivative = derivative;
derivative = neuron_delta * pre->Output();
}
// [...]
// [...]
void neuron::AcquiringDeltaError(void)
{
double accumulator = 0;
for(uint i = 0; i < OutSynapses.size(); i++)
{
accumulator += (OutSynapses[i]->GetWeight() * OutSynapses[i]->GetPostNeuron()->GetDelta());
}
Error = accumulator;
}
// [...]
// [...]
void BackPropagation::OnLineLearning(void)
{
for(uint o = 0; o < network->GetOutputNeurons()->size(); o++)
{
for(uint s = 0; s < network->GetOutputNeuronAt(o)->GetInSyn()->size(); s++)
{
network->GetOutputNeuronAt(o)->GetSynapseAt(s)->SetUpdateWeight(
learning_rate * network->GetOutputNeuronAt(o)->GetSynapseAt(s)->GetDerivative());
}
}
for(uint h = 0; h < network->GetHiddenLayers()->size(); h++)
{
for(uint n = 0; n < network->GetHiddenLayerAt(h)->GetNeurons()->size(); n++)
{
if(!network->GetHiddenLayerAt(h)->GetNeuronAt(n)->IsBiasNeuron())
{
for(uint s = 0; s < network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetInSyn()->size(); s++)
{
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetSynapseAt(s)->SetUpdateWeight(
learning_rate * network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetSynapseAt(s)->GetDerivative());
}
}
}
}
}
// [...]
// [...]
void PropagationBase::Adjust(void)
{
// Adjust all weights after learning process
for(uint o = 0; o < network->GetOutputNeurons()->size(); o++)
{
if(!network->GetOutputNeuronAt(o)->IsBiasNeuron())
{
for(uint s = 0; s < network->GetOutputNeuronAt(o)->GetInSyn()->size(); s++)
{
network->GetOutputNeuronAt(o)->GetSynapseAt(s)->AddMomentum(beta);
network->GetOutputNeuronAt(o)->GetSynapseAt(s)->Update();
}
}
}
for(uint h = 0; h < network->GetHiddenLayers()->size(); h++)
{
for(uint n = 0; n < network->GetHiddenLayerAt(h)->GetNeurons()->size(); n++)
{
if(!network->GetHiddenLayerAt(h)->GetNeuronAt(n)->IsBiasNeuron())
{
for(uint s = 0; s < network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetInSyn()->size(); s++)
{
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetSynapseAt(s)->AddMomentum(beta);
network->GetHiddenLayerAt(h)->GetNeuronAt(n)->GetSynapseAt(s)->Update();
}
}
}
}
}
// [...]
[La libreria non è opensource, scritta in C++ 11 estendibile e cross-platform. Comprende configurazioni e metodi di addestramento: feed-forward, M-Adeline, Self-organizing, simulated-annealing, ART, Recurrent feed-forward e algoritmi genetici. Aziende e/o privati interessati mi possono contattare direttamente tramite mail disponibile nella sezione "About".]
Per collaudare l’algoritmo addestriamo una rete neurale per risolvere il problema XOR, un problema che presenta soluzioni non linearmente separabili, quindi che necessita di una rete più complessa del perceptron. Il seguente codice di esempio, utilizza la libreria per implementare la dimostrazione, inoltre, utilizzando il vettore di debug per l’errore, possiamo osservare la discesa del valore MSE, nonchè, verificare le prestazioni di BACKPROP. N.B. L’algoritmo BACKPROP non assicura la convergenza alla soluzione, questo dipende dall’inizializzazione dei valori sinaptici.
#include "stdafx.h"
#include "libsann.h"
#include <stdio.h>
#include <fstream>
#include <iostream>
using namespace libsann;
int _tmain(int argc, _TCHAR* argv[])
{
INIT
double** input = (double**)malloc(sizeof(double*)*4);
double** output = (double**)malloc(sizeof(double*)*4);
for(uint i = 0; i < 4; i++)
{
input[i] = (double*)malloc(sizeof(double)*2);
output[i] = (double*)malloc(sizeof(double));
}
input[0][0] = 0.0; input[0][1] = 0.0;
input[1][0] = 0.0; input[1][1] = 1.0;
input[2][0] = 1.0; input[2][1] = 0.0;
input[3][0] = 1.0; input[3][1] = 1.0;
output[0][0] = 0.0;
output[1][0] = 1.0;
output[2][0] = 1.0;
output[3][0] = 0.0;
// Build the XOR training set
Trainingset *exampleSet = new Trainingset(input,output,4,2,1);
// Create a vector of hidden layers: 1 hidden layer with two neurons
vector<FeedForwardLayer*> LayersHidden;
LayersHidden.push_back(new FeedForwardLayer(2));
// Create the ANN
Mlp *net = new Mlp(
new InputLayer(2),
LayersHidden,
new FeedForwardLayer(1)
);
// Connects the units
net->BuildNet(true);
// Build training method
BackPropagation *train = new BackPropagation(net,0.01,10000,0.5,0.5);
//ResilientPropagation *train = new ResilientPropagation(net,0.01,10000);
// Train
train->SetTrainingSet(exampleSet);
train->Training(false);
// Write the errors to file for debug purpose
ofstream myfile;
myfile.open("Error_net.csv");
for(uint i = 0; i < train->_DEBUG_net_error_v.size(); i++)
myfile << train->_DEBUG_net_error_v[i] << ";" << endl;
myfile.close();
}
In questo esempio ho utilizzato una rete MLP con 2 neuroni nascosti, un learning rate pari a 0,5 e il coefficente momentum a 0,5. Di seguito riporto una serie di test che danno l’idea delle prestazioni di BACKPROP utilizzando diverse configurazioni di una rete MLP. Nei grafici è visualizzata la discesa dell’errore quadratico medio, per ogni configurazione ho eseguito 4 test.
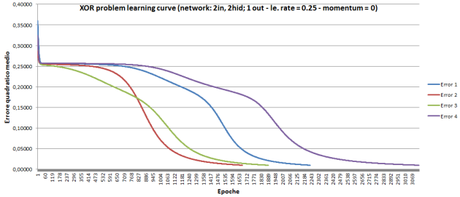
Figura 3: BACKPROP – Discesa MSE 2 input, 2 hidden, 1 output, l.rate = 0.25
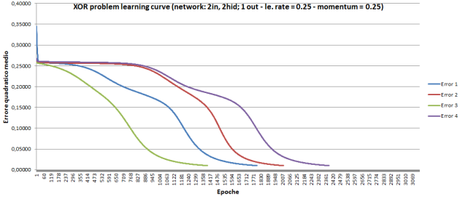
Figura 4: BACKPROP – Discesa MSE 2 input, 2 hidden, 1 output, l.rate = 0.25, momentum k = 0.25
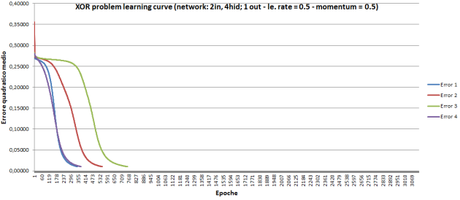
Figura 5: BACKPROP – Discesa MSE 2 input, 4 hidden, 1 output, l.rate = 0.5, momentum k = 0.5
La terza configurazione è quella decisamente più performante.
Tuttavia, molti studi successivi al 1986 hanno evidenziato varie problematiche di BACKPROP, in primis, il problema dei minimi locali. Ovvero, per molte combinazioni di pesi sinaptici esistono soluzioni che si avvicinano ma non raggiungono la soluzione ottimale. Nella discesa del gradiente l’errore può essere rappresentato come una pallina che scorre su una superfice curva e che si trova davanti vari avvallamenti. L’algoritmo BACKPROP non ha un metodo efficente per uscire dai falsi minimi. Tale problema è stato in parte limitato da alcune soluzioni successive e eliminato completamente con sistemi di addestramento alternativi, come quelli genetici, ma che non tratteremo in questo articolo.
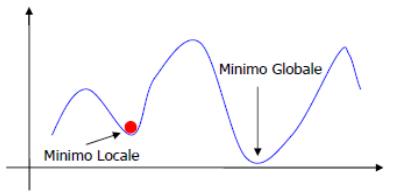
Figura 6: Minimo locale e minimo globale
Un’altra inconvenienza di BACKPROP è la sua lentezza e dispendiosità in termini di elaborazione. Come nel seguente caso, BACKPROP può rallentare molto e impiegare molto tempo per convergere correttamente verso la soluzione.
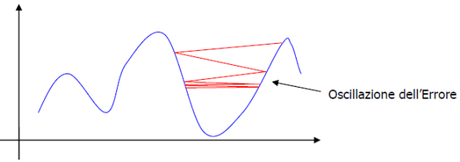
Figura 8: Algoritmo BACKPROP su un minimo
Una delle varianti di BACKPROP che ha avuto miglior successo è l’algoritmo “Resilient Propagation” [2].
L’algoritmo mantiene lo stesso procedimento di BACKPROP per calcolare gli errori e le derivate di ogni neurone, ma utilizza dei valori fissi adattivi e locali ad ogni connessione per modificare il valore di aggiornamento. Inoltre, non utilizza il valore della derivata ma solo il suo segno per determinare se il peso verrà aumentato o diminuito. Per capire il ragionamento su cui poggia questo algoritmo dobbiamo ragionare sull’andamento della derivata durante il processo di addestramento.
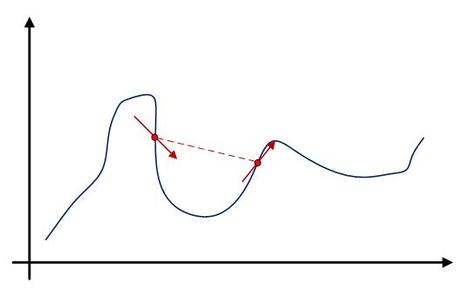
Figura 9: Andamento della derivata dell’errore
Infatti, quando la derivata cambia di segno, significa che l’algoritmo ha saltato sopra un minimo. In questo caso Resilient Propagation (RPROP), decrementa il valore di aggiornamento in modo che alla prossima iterazione il salto sia più piccolo e la discesa prosegua verso il minimo. Si veda meglio in [2].
Meglio dicendo, RPROP introduce per ogni peso sinaptico W un fattore di aggiornamento individuale che determina la dimensione di aggiornamento del peso. Esso evolve durante il processo di apprendimento aumentando o diminuendo il suo valore basandosi sulla funzione d’errore E, formalizzando:
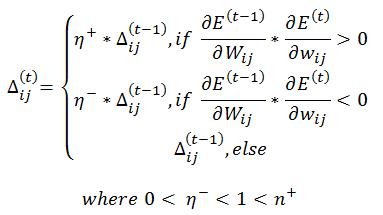
Una volta che il valore di aggiornamento è stato adattato, l’aggiornamento dei pesi segue questa regola molto semplice: Se la derivata è positiva (aumento dell’errore) il valore viene sottratto, altrimenti viene aggiunto. In formule:
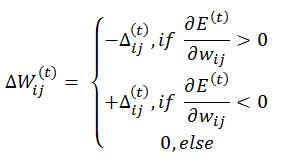
Inoltre c’è una eccezione: Se la derivata cambia segno e per esempio, il precedente step di aggiornamento è stato molto grande, il minimo è stato perso, allora il precedente aggiornamento viene sottratto. (si torna indietro)
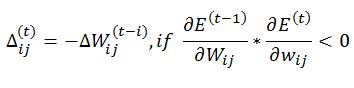
Per evitare che venga doppiamente penalizzato il peso durante il successivo aggiornamento, il valore di aggiornamento non viene aggiornato nello step successivo, generalmente questo si fa settando a 0 la derivata precedente. Per meglio comprendere RPROP, formalizzando quanto detto si ha l’algoritmo:
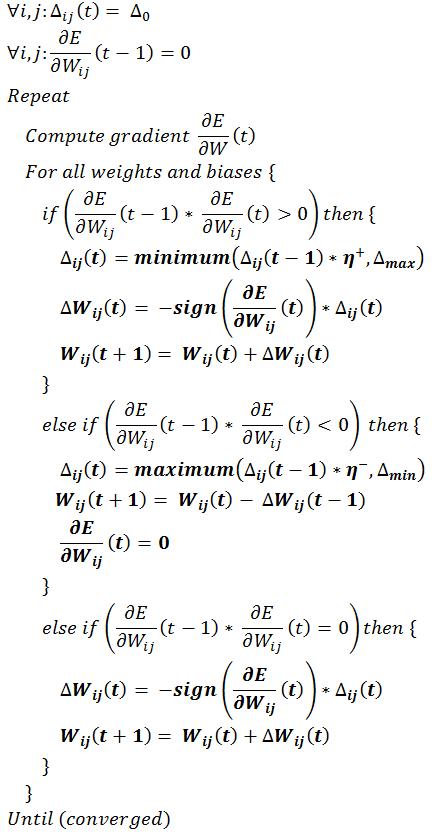
All’inizio, i valori di aggiornamento sono settati a 0,1. Questo valore comunque non dovrebbe essere critico, qualsiasi valore iniziale va bene e non ostacola la convergenza. I valori delta massimo e minimo utilizzati nello pseudocodice servono per porre un limite inferiore e superiore all’aggiornamento. Solitamente si utilizza un massimo pari a 50.0 e un minimo pari a e^-6. I valori di incremento e decremento della variabile di aggiornamento sono solitamente settati a 1,5 e 0,5 rispettivamente.
Il successo di RPROP è dovuto al concetto di adattamento diretto della dimensione del valore di aggiornamento. Test pratici dimostrano che RPROP è attualmente il miglior algoritmo di addestramento per reti neurali feed-forward a più livelli.
Di seguito sono riportati i risultati ottenuti con RPROP nel test con qui abbiamo in precedenza verificato le prestazioni di BACKPROP. Deve essere fatta particolare attenzione alla scala, RPROP converge nel migliore dei test eseguiti in 48 epoche, mentre BACKPROP nel migliore dei casi necessitava di 351 epoche.
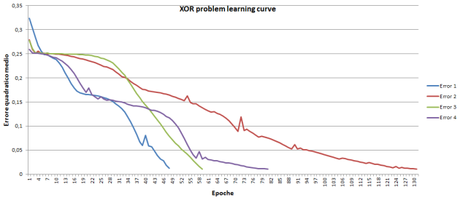
Figura 10: RPROP- Discesa MSE 2 input, 2 hidden, 1 output
Molte altre varianti di BACKPROP con cui si ottengono ottimi risultati fanno uso di learning rate locale, e modificano il peso delle sinapsi basandosi sul segno della derivata e non sul suo valore, sembra essere questo uno dei paradigmi più efficienti sino ad oggi.
Bibliografia
.1 Arthur Earl Bryson, Yu-Chi Ho – Applied optimal control: optimization, estimation, and control. Blaisdell Publishing Company or Xerox College Publishing. p. 481, 1969
.2 Martin Riedmiller, Heinrich Braun - A Direct Adaptive Method for Faster Backpropagation Learning, University of Karlsruhe
.3 Silvio Cammarata – Reti neuronali. Dal perceptron alle reti caotiche e neuro-fuzzy, ETASLIBRI, 1990
.4 Andres Reyes – Ciò che l’occhio della rana comunica al cervello della rana: da Kant alle reti neurali artificiali, EOS elettronica open source, 2012
.5 Alpaydın, Ethem – Introduction to machine learning, Cambridge, Mass.: MIT Press. 1986
.6 Donald Hebb – The Organization of Behavior: A Neuropsychological Theory, 1949






