Come sapere quanto è alto un albero (metodi pratici)

CALCOLARE - MISURARE - STIMARE L'ALTEZZA DEGLI ALBERI Primo metodo

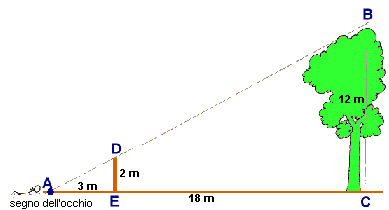
Pianta per terra un picchetto di cui conosci l'altezza (es. 2 m) Sdraiati per terra. Mettiti ad una distanza dall'albero maggiore di quella che pensi sia l'altezza dell'albero Guarda tenendo la testa sul suolo, e spostati finchè non vedi coincidere la cima del picchetto e quella dell'albero Segna sul terreno il punto esatto in cui questo avviene (punto A) Misura sul terreno la distanza tra questo punto e l'albero (nel nostro esempio 18 m, segmento AC) e la distanza tra il punto e la base del picchetto (segmento AE) I due triangoli ABC e ADE sono simili, perchè triangoli rettangoli che hanno lo stesso angolo A. Per sapere l'altezza moltiplica la distanza che c'è tra picchetto e albero per l'altezza del picchetto, poi dividi per la distanza che c'è tra te e il picchetto. Cioè AC:AE = BC:DE, e la grandezza che cerchiamo, BC= (ACxDE): AE Nell'esempio riportato quindi (18x2):3 = 12 m Secondo metodo

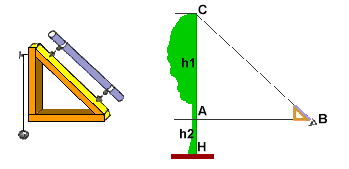
Costruisci con tre assicelle di legno un triangolo rettangolo isoscele di 25 cm di lato circa. Fissa con la colla un tubo di plastica di circa 1.5 cm di diametro sul lato più lungo del triangolo. Fissa su un lato verticale del triangolo un filo a piombo, o metti una livella su quello orizzontale. Il tuo strumento si chiama dendrometro Disponi lo strumento all'altezza degli occhi Verifica che sia perfettamente orizzontale con il filo a piombo Mettiti in modo da vedere la sommità dell'albero usando il mirino costituito dal cilindro di plastica Misura la distanza che c'è tra la punta del dendrometro e la base dell'albero Poichè ABC è un triangolo rettangolo isoscele AB=AC, l'altezza dell'albero (CH) è uguale ad AB+AH Terzo metodo   


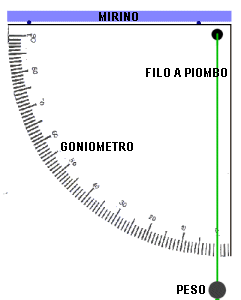
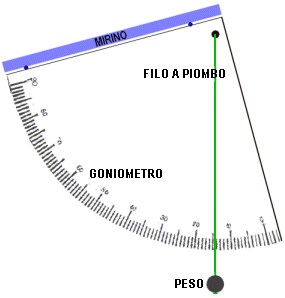
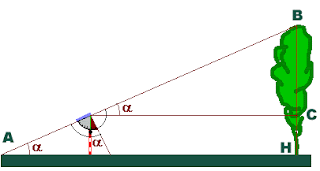
Questo metodo è utile quando non ci si può appiattire per terra o non si può scegliere una posizione determinata dall'albero (ad esempio per la presenza di cespugli o siepi). Presuppone la conoscenza di qualche nozione di geometria e di trigonometria. Incollare un quadrante da 0° a 90° di un goniometro su un pezzo di compensato o di cartone di circa 20x30 cm. Alternativamente fare una fotocopia del goniometro e incollare quella. Segare o ritagliare con precisione lungo il contorno curvo. Incollare sullo spessore del supporto il mirino costituito da una cannuccia o dal guscio vuoto di un pennarello Fare un piccolo foro al vertice dell'angolo Infilare il filo a piombo nel foro e legarlo Attraverso una vite passante fissare il goniometro su un paletto di altezza nota, ad esempio 1.5 m Misurare l'angolo sotto cui si vede la cima dell'albero (angolo alfa BDC) Misurare la distanza al piede dell'albero (HK) Misurare l'altezza del paletto (DK) L'altezza dell'albero è BH = BC+CH e BC = DB x senBDC. Il segmento DC = DB x cosBDC, quindi DB = AC : cosBDC. BC è dunque DC x (senBDC : cos BDC), quindi sommando al risultato l'altezza CH si ottiene l'altezza dell'albero (BH). Seno e coseno di un angolo possono esser calcolati con una calcolatrice che abbia quelle funzioni, che purtroppo mancano da quella presente in quasi tutti i PC e che si trova sotto la voce "accessori" del menù di avvio. E' possibile semplificare questi calcoli se possiamo scegliere l'angolo BDC. Se ad esempio fosse 60°, BH=(DC x 1.72) + CH, se di 30° BH=(DC x 0.58) + CH, se di 25° BH=(DC x 0.46) Quarto metodo

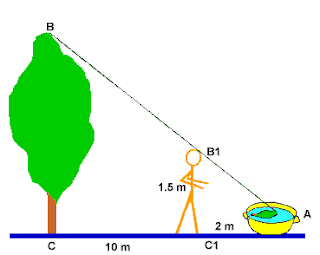
Devi sapere la tua altezza altezza B'C' (nel nostro esempio 1.5 m) Sistema una bacinella piena d'acqua sul terreno, anche qui ad una distanza maggiore da quella che si suppone essere l'altezza dell'albero Misura la distanza AC (nell'esempio 10 m) Spostati in modo da vedere la sommità dell'albero riflessa nella bacinella, e misura la tua distanza da quest'ultima AC' (nel nostro esempio 2 m)
Anche in questo caso i triangoli ABC e A'B'C' sono simili, quindi BC:B'C' = AC:AC'; la grandezza che cerchiamo, BC = (ACxB'C'):AC' (nel nostro esempio BC=7.5 m)