Correlazione della funzione zeta di Riemann con sistemi fisici del tipo "oscillatore armonico"

Pensavo di aver scoperto l'acqua calda, nel senso che se ho una funzione (reale di una variabile reale) che si annulla infinite volte, le possibilità sono due: 1) la funzione è identicamente nulla (in tal caso l'insieme degli zeri si identifica con l'asse x); 2) la funzione ha un comportamento oscillante (non necessariamente periodico). È chiaro che nel caso 2 si può comunque scrivere un'equazione differenziale del tipo oscillatore armonico, eventualmente con frequenza variabile in modo da riprodurre la non periodicità della funzione.

Ma ripetendo le simulazioni su luoghi geometrici differenti dalla famigerata linea critica, ho ritrovato il comportamento oscillante. Naturalmente, in questo caso le oscillazioni sono tali che le due funzioni (parte reale e parte immaginaria della zeta calcolata sul luogo geometrico) NON hanno zeri in comune (e ciò corrobora l'ipotesi di Riemann). Ad esempio, ho provato a utilizzare come luogo geometrico regolare, la circonferenza di raggio 1/3 e centrata nell'origine. SORPRESA: nel piano di Riemann (csi,eta) la traiettoria è una circonferenza. Le due funzioni oscillano, ma non sono quelle dell'oscillatore armonico, per cui il moto risultante è si circolare, ma non uniforme.
Per ultimo, ho provato sulla retta simmetrica (rispetto all'asse delle ordinate) della linea critica, cioè la retta di equazione x=-1/2, ottenendo la traiettoria:

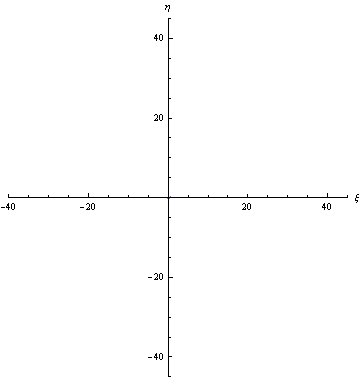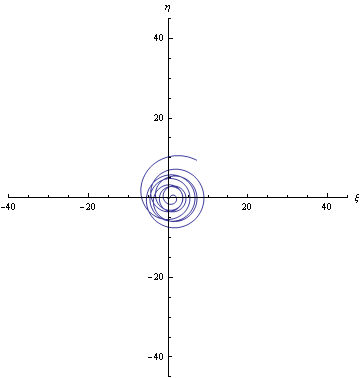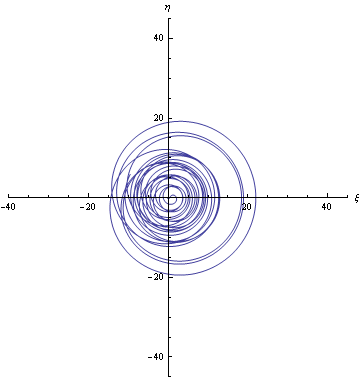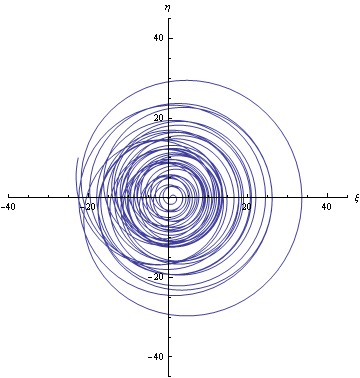
Qui vediamo che la particella si allontana definitivamente dall'origine (senza mai passarci), per cui non ci sono zeri della zeta lungo questa retta.

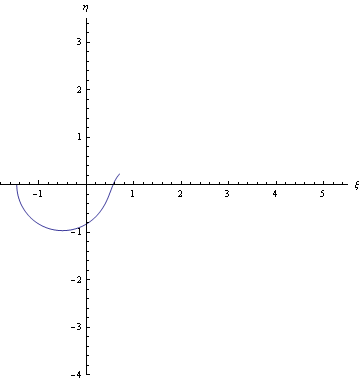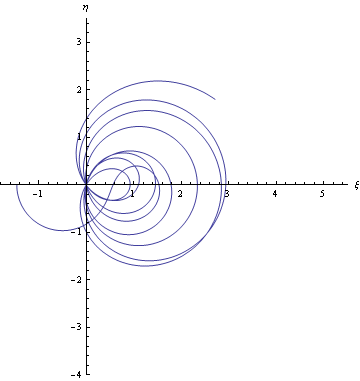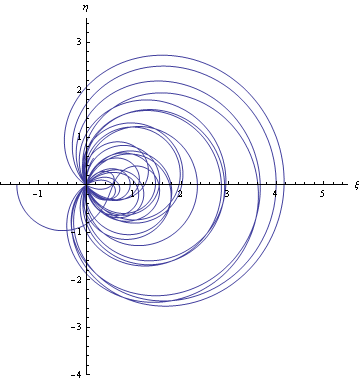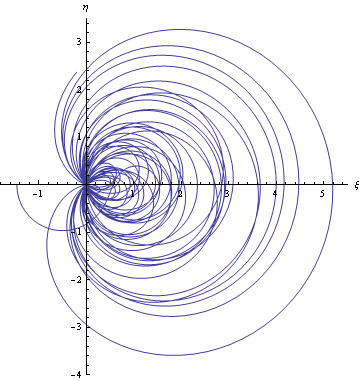
Ricordo che nel caso della linea critica, si ottiene l'andamento opposto:

Per concludere (per ora), penso che il "mago della situazione" sia rappresentato da questi due oggetti:

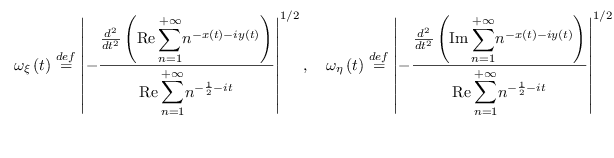
Possiamo congetturare che nel caso della zeta di Riemann, tali funzioni siano 1) Reali; 2) Positive. In altri termini, le suddette funzioni svolgono il ruolo della frequenza di un oscillatore armonico (per inciso, per la presenza del modulo, le due grandezze sono non negative. Tuttavia la nostra richiesta è che siano non nulle, altrimenti l'oscillatore degenera in una particella che compie un moto rettilineo ed uniforme, cosa che non succede con la zeta di Riemann) E dalla loro espressione mi aspetto che siano la parte reale e la parte immaginari di particolari serie di Dirichlet. Cioè:

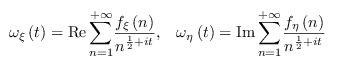
Ne consegue che la funzione zeta di Riemann ingloba un numero infinito non numerabile di oscillatori armonici 2-dimensionali, ciascuno per ogni curva regolare del piano complesso su cui vengono mappate la parte reale e la parte immaginaria della zeta. Inoltre, esiste ed è unico l'oscillatore che passa infinite volte per l'origine. Tale oscillatore corrisponde alla linea critica.