Definizione di limite di una funzione reale di una variabile reale (con Mathematica)

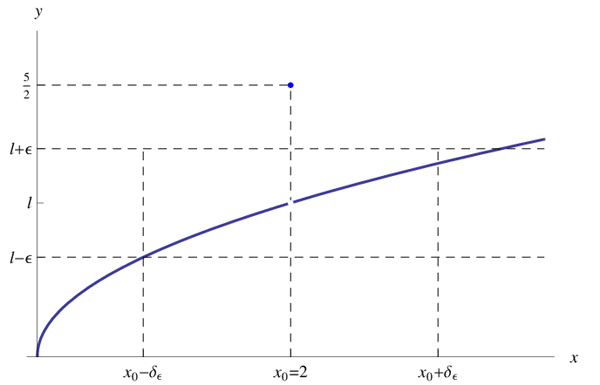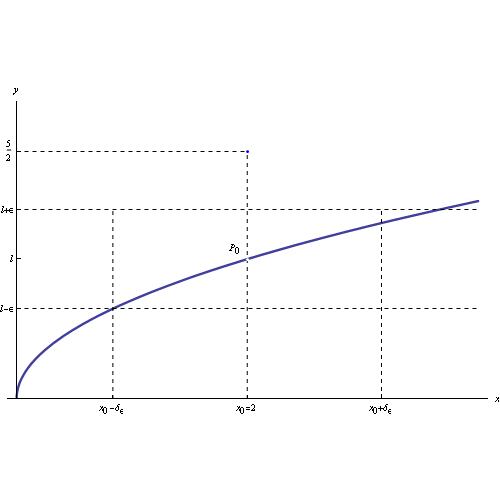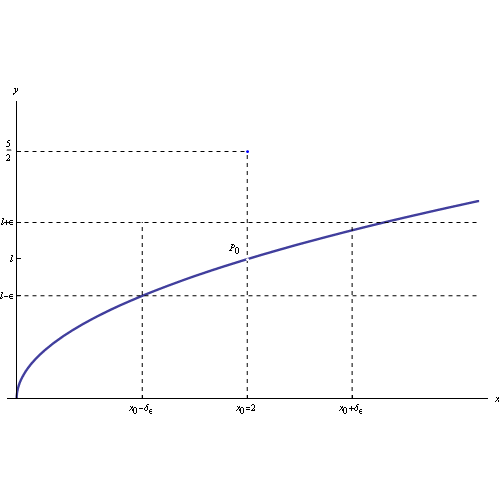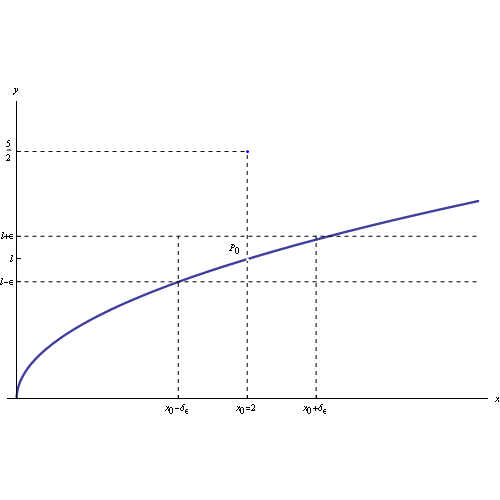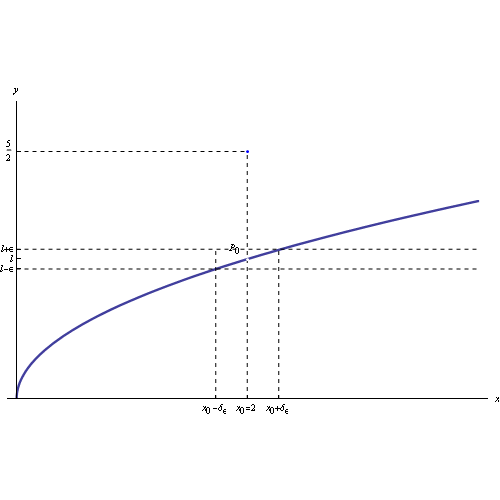
Assegnata una funzione reale di una variabile reale f(x), diremo che tale funzione tende al limite l per x->0, dove x0 è un punto di accumulazione per il campo di esistenza di f, se possiamo rendere arbitrariamente piccola la differenza |f(x)-l|, a patto di prendere x sufficientemente prossimo a x0. Più rigorosamente:

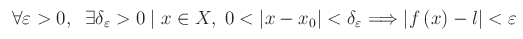
Quindi scriviamo:

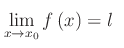
Ad esempio:

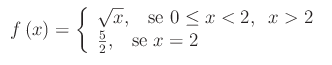
Otteniamo:

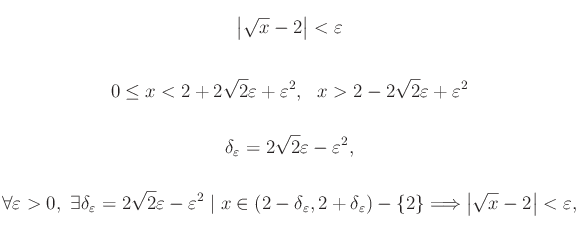
Ne consegue che i punti del grafico della funzione appartenenti al prodotto cartesiano dei predetti intorni, sono contenuti in un rettangolo centrato in P0(x0,l), come illustrato in fig: