Nel post precedente abbiamo visto l'esempio di una funzione non derivabile in x=0, in quanto il rapporto incrementale oscillava tra -1 e +1, al tendere a zero dell'incremento della variabile indipendente.
Oggi esaminiamo il caso di una funzione il cui rapporto incrementale non è regolare al tendere a zero dell'incremento della variabile indipendente, ma è convergente a sinistra e a destra. Più precisamente, si ha:
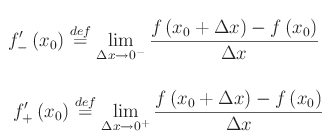
La funzione presa come esempio è f(x)=|sin(x)|. In tal caso riesce:
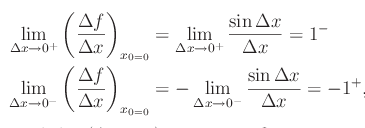
Cioè la derivata prima ha una discontinuità di prima specie in x=0. In tal caso si dice che la funzione è derivabile a sinistra e a destra in x=0 (ovviamente non è ivi derivabile, giacchè il rapporto incrementale tende a due limiti distinti, a seconda di come "ci avviciniamo" a Delta_x=0). Il risultato finale è:
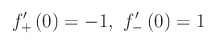
A questo punto diventa istruttivo passare tutte queste info a Mathematica, per poi generare un'animazione. Osserviamo innanzitutto che Mathematica non calcola la derivata di una funzione la cui espressione contiene il valore assoluto.
In altre parole, se scriviamo Abs[Sin[x]], il kernel restituisce Abs'[Sin[x]]. Probabilmente esiste qualche trucco per risolvere il problema. Tuttavia, ho utilizzato il comando Piecewise per scrivere la restrizione a (-pi,pi) (anche se poi la funzione è periodica di periodo T=pi):
Scriviamo quindi il rapporto incrementale:
Ora non dobbiamo fare altro che utilizzare lo script di qualche post fa, ovvero, dopo aver caricato il package "PlotLegends":
Scriamo la solita Table[] per poi esportare in gif, ottenendo la fig. al top di questa pagina.
Pacman
Nostradamus
Magical Cat Adventure
Snake