Dimostrazione per assurdo del Teorema di unicità del limite

Se f è una funzione reale definita in X sottoinsieme del campo reale e x₀ un punto di accumulazione per X, il teorema di unicità del limite afferma

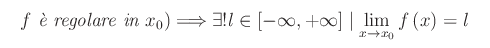
Dimostrazione.
Procediamo per assurdo, negando la tesi (senza perdita di generalità supponiamo che x₀ sia di accumulazione al finito e che la funzione sia convergente):

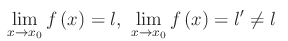
Per definizione di limite:

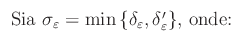
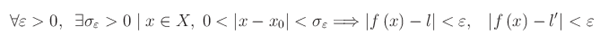
Cioè:

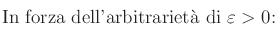
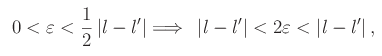
da cui la disuguaglianza assurda |l-l'|<|l-l'|, onde la tesi. c.d.d.

Da un punto di vista numerico/computazionale possiamo verificare tale teorema nel caso di una funzione assegnata, per poi assegnare il valore di l'. Con Mathematica, ad esempio, otteniamo l'animazione grafica riportata al top in cui vediamoche per l' la definzione di limite è violata. Qui il file pdf contenente il codice Mathematica.