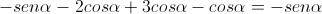Risolviamo 2
espressioni goniometriche mediante l'impiego degli
angoli associati, che spesso in goniometria si rivelano di grande aiuto.
Ecco la prima:
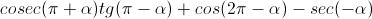
Trasformiamo secante e cosecante rispettivamente in funzione di coseno e seno, tenendo conto che
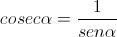
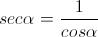
Avremo quindi:
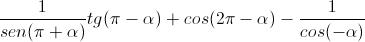

Adesso possiamo semplificare l'espressione
ricordando le relazioni esistenti tra le funzioni goniometriche di un angolo e quelle dei suoi angoli associati. In particolare:
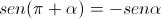
(perché sono angoli che differiscono di un angolo piatto, ed hanno quindi seno opposto);
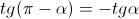
(perché angoli supplementari hanno uguale seno e coseno opposto, quindi tangente opposta);
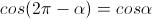
(perché angoli esplementari hanno uguale coseno);
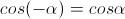
(perché angoli opposti hanno uguale coseno).
L'espressione diventerà:
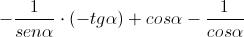
Esprimiamo la tangente come rapporto tra seno e coseno:
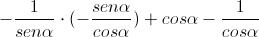
Semplifichiamo:
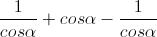
Eliminiamo i termini opposti e otterremo come risultato:
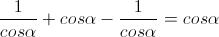
Ed ora
risolviamo la seconda:
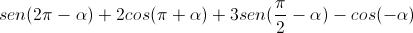 Effettuiamo le seguenti sostituzioni ricordando alcune relazioni esistenti con gli angoli associati corrispondenti:
Effettuiamo le seguenti sostituzioni ricordando alcune relazioni esistenti con gli angoli associati corrispondenti:
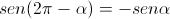
(perché angoli esplementari hanno coseno opposto)
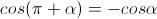
(perché angoli che differiscono di un angolo piatto hanno coseno opposto)
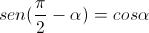
(perché il seno di un angolo è uguale al coseno dell'angolo complementare)
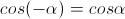
(perché angoli opposti hanno coseno opposto)
Otteniamo:
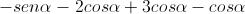
Semplificando i restanti calcoli, avremo:
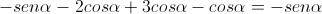
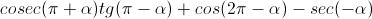 Trasformiamo secante e cosecante rispettivamente in funzione di coseno e seno, tenendo conto che
Trasformiamo secante e cosecante rispettivamente in funzione di coseno e seno, tenendo conto che
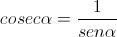
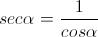 Avremo quindi:
Avremo quindi:
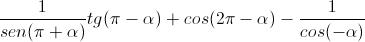
 Adesso possiamo semplificare l'espressione ricordando le relazioni esistenti tra le funzioni goniometriche di un angolo e quelle dei suoi angoli associati. In particolare:
Adesso possiamo semplificare l'espressione ricordando le relazioni esistenti tra le funzioni goniometriche di un angolo e quelle dei suoi angoli associati. In particolare:
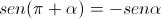 (perché sono angoli che differiscono di un angolo piatto, ed hanno quindi seno opposto);
(perché sono angoli che differiscono di un angolo piatto, ed hanno quindi seno opposto);
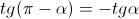 (perché angoli supplementari hanno uguale seno e coseno opposto, quindi tangente opposta);
(perché angoli supplementari hanno uguale seno e coseno opposto, quindi tangente opposta);
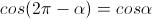 (perché angoli esplementari hanno uguale coseno);
(perché angoli esplementari hanno uguale coseno);
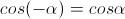 (perché angoli opposti hanno uguale coseno).
L'espressione diventerà:
(perché angoli opposti hanno uguale coseno).
L'espressione diventerà:
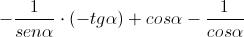 Esprimiamo la tangente come rapporto tra seno e coseno:
Esprimiamo la tangente come rapporto tra seno e coseno:
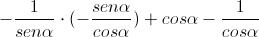 Semplifichiamo:
Semplifichiamo:
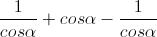 Eliminiamo i termini opposti e otterremo come risultato:
Eliminiamo i termini opposti e otterremo come risultato:
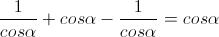 Ed ora risolviamo la seconda:
Ed ora risolviamo la seconda:
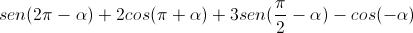 Effettuiamo le seguenti sostituzioni ricordando alcune relazioni esistenti con gli angoli associati corrispondenti:
Effettuiamo le seguenti sostituzioni ricordando alcune relazioni esistenti con gli angoli associati corrispondenti:
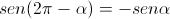 (perché angoli esplementari hanno coseno opposto)
(perché angoli esplementari hanno coseno opposto)
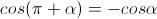 (perché angoli che differiscono di un angolo piatto hanno coseno opposto)
(perché angoli che differiscono di un angolo piatto hanno coseno opposto)
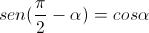 (perché il seno di un angolo è uguale al coseno dell'angolo complementare)
(perché il seno di un angolo è uguale al coseno dell'angolo complementare)
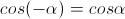 (perché angoli opposti hanno coseno opposto)
Otteniamo:
(perché angoli opposti hanno coseno opposto)
Otteniamo:
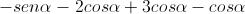 Semplificando i restanti calcoli, avremo:
Semplificando i restanti calcoli, avremo: