Abbiamo già visto in alcuni post degli esempi di risoluzioni guidate di espressioni algebriche contenenti prodotti notevoli di polinomi, come questo, in cui ci sono sia il quadrato di binomio sia prodotto di somma per differenza di termini, oppure quest'altro, in cui sono anche presenti esponenti letterali. Vediamone ora un terzo esempio, contenente come prodotti notevoli sia il quadrato di binomio che il prodotto tra somma e differenza di termini:![\left [ 8a^2+(a+2)^2\cdot (a-2)^2-(a^2+4)^2 \right ]^2\cdot(a-1)+8\cdot(-a^2)^2\cdot(8-9a) Espressione algebrica con polinomi (prodotti notevoli) 2](//m2.paperblog.com/i/214/2145882/espressione-algebrica-con-polinomi-prodotti-n-L-LjR3hD.jpeg)
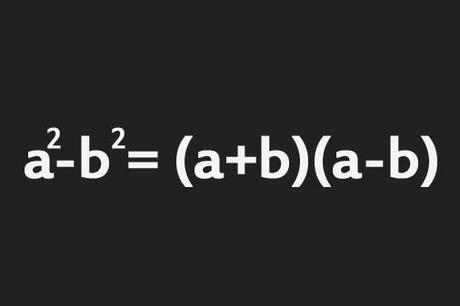
Prodotto notevole del tipo
"somma per differenza" dei termini
Osserviamo che il prodotto tra (a+2)^2 e (a-2)^2 è il prodotto tra 2 potenze aventi uguale esponente, per cui esso, per le proprietà delle potenze, non sarà altro che una potenza avente come esponente lo stesso esponente e come base il prodotto tra le basi; le basi, a loro volta, sono la somma e differenza tra gli stessi termini, per cui (a+2) per (a-2) rappresentano un prodotto notevole del tipo (a+b) per (a-b) come in figura accanto. Svolgiamo anche la potenza nella penultima parentesi tonda, ricordando che, se l'esponente è pari, la potenza risultante è sempre positiva.Avremo quindi:Sviluppiamo il quadrato di binomio in parentesi:Eliminiamo tutti i termini opposti nella parentesi quadra e l'espressione diventerà:
Svolgiamo la prima potenza:
Eliminiamo le parentesi ed eseguiamo le moltiplicazioni tra i monomi fuori parentesi e ciascun termine dei binomi in parentesi:
![\left [ 8a^2+(a+2)^2\cdot (a-2)^2-(a^2+4)^2 \right ]^2\cdot(a-1)+8\cdot(-a^2)^2\cdot(8-9a) Espressione algebrica con polinomi (prodotti notevoli) 2](http://m2.paperblog.com/i/214/2145882/espressione-algebrica-con-polinomi-prodotti-n-L-LjR3hD.jpeg)
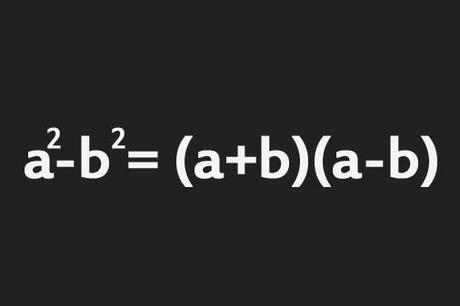
![[8a^2+(a^2-4)^2-a^4-8a^2-16]^2\cdot(a-1)+8\cdot (+a^4)\cdot (8-9a) Espressione algebrica con polinomi (prodotti notevoli) 2](http://m2.paperblog.com/i/214/2145882/espressione-algebrica-con-polinomi-prodotti-n-L-77olX6.jpeg)
![[8a^2+a^4-8a^2+16-a^4-8a^2-16]^2\cdot(a-1)+8a^4\cdot (8-9a) Espressione algebrica con polinomi (prodotti notevoli) 2](http://m2.paperblog.com/i/214/2145882/espressione-algebrica-con-polinomi-prodotti-n-L-ehxW3d.jpeg)
![[-8a^2]^2\cdot(a-1)+8a^4\cdot (8-9a) Espressione algebrica con polinomi (prodotti notevoli) 2](http://m2.paperblog.com/i/214/2145882/espressione-algebrica-con-polinomi-prodotti-n-L-jDgvaM.jpeg)



