Funzione convergente all'infinito. Il caso della salita esponenziale

La salita esponenziale è la seguente funzione reale della variabile reale x:

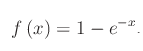
Congetturiamo:

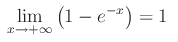
Applicando la definizione di limite, arriviamo alla seguente disequazione:

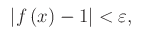
Cioè:

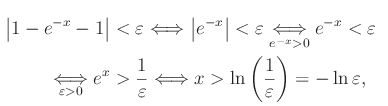
per cui

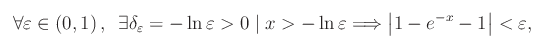
onde la correttezza della nostra congettura. Il grafico seguente contiene l'interpretazione geometrica della convergenza della funzione assegnata per x->+oo. La retta orizzontale y=l, si dice asintoto orizzontale a destra per il grafico della funzione.