Guida all’uso di MatLab: come lavorare con le matrici.

Questa sezione presenta altri modi di creare matrici.

Generazione di matrici.

MATLAB prevede quattro funzioni che generano matrici di base. Degli esempi sono:

Z = zeros(2,4) Z =

0 0 0 0

0 0 0 0

F = 5*ones(3,3) F =

5 5 5

5 5 5

5 5 5

N = fix(10*rand(1,10)) N =

4 9 4 4 8 5 2 6 8 0

R = randn(4,4) R =

1.0668 0.2944 -0.6918 -1.4410

0.0593 -1.3362 0.8580 0.5711

-0.0956 0.7143 1.2540 -0.3999

-0.8323 1.6236 -1.5937 0.6900

zeros All zeros

ones All ones

rand Uniformly distributed random elements

randn Normally distributed random elements.

Manipolare le matrici.

Poniamo l’attenzione su alcune funzioni che consentono di manipolare matrici e vettori.

abs

Applicata ad una matrice reale, produce la matrice dei valori assoluti. Applicata ad un numero complesso, ne calcola il modulo.

Esempio:

z=3+i*4

z =

3.0000+ 4.0000i

abs(z)

ans =

5

tril (oppure triu)

Estraggono da una matrice la parte triangolare inferiore(superiore). Indicando un numero positivo o negativo come secondo argomento è possibile estrarre le altre diagonali della matrice. Ad esempio:

diag

Applicata ad una matrice ne estrae la diagonale,applicata ad un vettore crea una matrice diagonale.

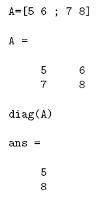
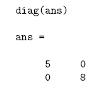
sum

Applicata ad una matrice fornisce un vettore che contiene le somme per colonna degli elementi della matrice; applicata ad un vettore fornisce uno scalare dato dalla somma degli elementi del vettore.

max (oppure min)

Se applicata ad un vettore calcola il massimo (rispettivamente il minimo) degli elementi di un vettore. Se applicata ad una matrice produce un vettore che contiene il massimo degli elementi della matrice per colonne.

norm

Calcola la norma 2 di un vettore o di una matrice. Inoltre, norm (A, inf) calcola la norma infinito di A, mentre norm (A, 1) calcola la norma 1 di A.

cond

Calcola il numero di condizionamento in norma 2 di una matrice A.

eig

calcola gli autovalori di una matrice quadrata. Se richiamata nel modo seguente [X, D] =eig (A) produce una matrice diagonale D che contiene gli autovalori di A e la matrice X le cui colonne sono gli autovettori di A.