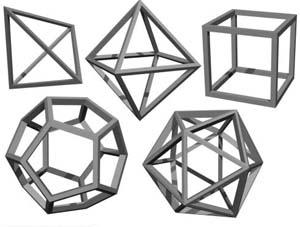
I Solidi Platonici In Video

I Solidi platonici in video  costituiscono una risorsa molto utile per comprendere la struttura dei 5 poliedri regolari: tetraedro, esaedro, ottaedro, dodecaedro e icosaedro
Ricordiamo brevemente che un poliedro si dice regolare se le sue facce sono poligoni regolari tutti congruenti tra loro, tutti i suoi diedri sono congruenti tra loro, tutti i suoi angoloidi sono congruenti tra loro. 
 Dei cinque poliedri regolari, tre sono formati da: 
- 4 triangoli equilateri congruenti (tetraedro regolare)
- 8 triangoli equilateri congruenti ( ottaedro regolare)
- 20 triangoli equilateri congruenti (icosaedro regolare)
Gli altri due sono l'esaedro regolare o cubo, formato da 6 quadrati congruenti, e il dodecaedro regolare, formato da 12 pentagoni congruenti.
Le facce dei poliedri regolari possono essere quindi solo di tre tipi: triangoli equilateri, quadrati, pentagoni regolari.
Ricordando, inoltre, che che la somma delle ampiezze delle facce di un angoloide deve essere sempre minore di 360°, possiamo anche essere certi che non possono esserci altri poliedri regolari a facce triangolari oltre a quelli già citati, che hanno rispettivamente gli angoloidi di 3, 4, 5 facce di 60° gradi ciascuna: un angoloide, formato da 6 facce di 60°, si schiaccerebbe infatti sul piano!
Per la stessa ragione, non possono esistere:
- oltre all'esaedro regolare, altri poliedri regolari a facce quadrate
- oltre al dodecaedro regolare, altri poliedri regolari a facce pentagonali
- poliedri regolari con facce esagonali, ettagonali ecc.
Il tetraedro regolare ha 4 facce congruenti (triangoli equilateri), 6 spigoli, 4 vertici.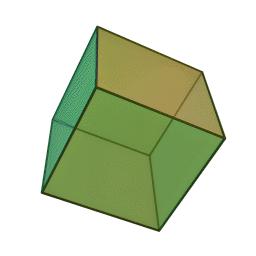
L'esaedro regolare (o cubo) ha 6 facce congruenti (quadrati), 12 spigoli e 8 vertici.

L'ottaedro regolare ha 8 facce congruenti (triangoli equilateri), 12 spigoli e 8 vertici.
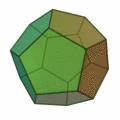Il dodecaedro regolare ha 12 facce congruenti (pentagoni regolari), 30 spigoli e 20 vertici.
 L'icosaedro regolare ha 20 facce congruenti (triangoli equilateri), 30 spigoli e 12 vertici.
 E adesso i video sui solidi platonici.
 Prima parte

Seconda parte

Concludo con il video di Peter Weatherall, divertente e istruttivo.

Post correlato:

Solidi Platonici, Microcosmo E Macrocosmo

(Le immagini gif dei solidi platonici sono presi da Wikipedia, mentre l'immagine statica dal sito Matematita)

AGGIORNAMENTO

Aggiorno il post con il commento di Aldo Bonet, che, come al solito, ci offre spunti di approfondimento.

Il fascino perpetuo di questi solidi regolari deve avere origini molto più antiche di Platone a cui si fanno risalire, forse già le scuole pitagoriche la cui la tradizione trae le sue radici dalle millenarie civiltà potamiche. Già nella natura della Magna Grecia si trovavano cristalli di pirite a forma di dodecaedro. Gli studi platonici certamente influenzarono Euclide, Archimede e questi di conseguenza, i matematici Pappo, Diofanto per poi arrivare, nel rinascimento, all’arte – matematica di Leonardo e per passare poi ai teorici della prospettiva, ripresi da Luca Pacioli nella sua Divina Proporzione. E ancora ne fu influenzata l’astronomia di Keplero nel rappresentare i pianeti, e lo studio delle relazioni che li lega grazie a René Descartes (Cartesio). E ancora Eulero, e l’arte di Salvador Dalì e molti altri. Ma anche nell’architettura recente ritroviamo il rombicubottaedro, ripreso dal ritratto di Luca Pacioli, e ancora nella struttura architettonica dell’imponente biblioteca di Minsk in Bielorussia.

Chi volesse trovare altri spunti sui solidi platonici, può leggere il libro di Piergiorgio Odifreddi: "Il grande racconto della geometria, c’è spazio per tutti". Mondadori editore. Un libro facile da leggere anche se vi sono descritti ed esposti considerazioni storiche che personalmente non condivido affatto. Per esempio, c’è una rappresentazione storico matematica distorta di Talete di Mileto che presenta i suoi teoremi come se fossero stati, dallo stesso Talete, studiati e scoperti con l’uso sistematico di riga-compasso e con uno spirito più astratto che concreto; spirito e strumenti invece ufficializzati soltanto dalle scuole di Platone e non certamente usati dalle scuole Ioniche di Talete, basate ancora su uno spirito essenzialmente pratico, com’era quello proprio dei milesi, poiché anche i primi pitagorici avevano ancora l’abitudine di disegnare sulla sabbia anziché sul più “moderno” papiro: l’internet dell’antichità.
Grazie Annarita per rinfrescarci sempre con questo intramontabile fascino che esercita la matematica in perpetuo moto dei sensi.
Aldo.

Grazie al commento di Aldo, ho cercato e trovato in rete un ottimo documento dell'unito, che vi propongo di seguito:

"Cenni di storia sui poliedri regolari"

 SECONDO AGGIORNAMENTO

Ancora un commento signifcativo di Aldo Bonet:

"Grazie Annarita per la tua integrazione e precisazione.
Per non far sola critica a Odifreddi, come poteva sembrare nel mio commento precedente, segnalo qui una sua frase del libro sopra indicato, pag. 111, che mi ha colpito molto:
“In ogni caso, qualcuno aveva già pensato al dodecaedro nel Neolitico, molto prima dei Pitagorici. Lo dimostra il ritrovamento, in una grotta scozzese, di centinaia di pietre sferiche lavorate risalenti a circa il -2000, e aventi le forme dei cinque solidi regolari di cui stiamo parlando. Esse dimostrano che non bisognerebbe assegnare agli Egizi, agli Indiani ai Greci il monopolio delle scoperte geometriche, né la loro primogenitura”
Possiamo qui essere d’accordo con Odifreddi. A mio parere, i Greci hanno attinto dalle civiltà potamiche, le quali, a loro volta, risalgono probabilmente da un’unica Civiltà Madre delle origini, dove il millenario diagramma d’argilla, da me ipotizzato, ha avuto un ruolo nevralgico nell’origine del pensiero algebrico-geometrico delle civiltà arcaiche.
Vorrei, qui riportare, una parte di pag. 39 del mio e-book: Lettera dello Scriba, che tu Annarita mi hai pubblicato su Calaméo, e far notare il punto 7:
“L’alba di quel luminoso giorno ha segnato l’inizio della storia dell’algebra e del pensiero algebrico che ha aperto le porte alla cultura matematica. L’accesso e la contemplazione verso questa straordinaria sezione modulare ha consentito all’uomo, dentro uno spirito “logico-enigmistico” forse nato per gioco e poi utilizzato didatticamente, di scoprire e di estrarre mediante problemi, i più grandi fondamenti algebrici e geometrici in essa contenuti:
1)La visualizzazione geometrica dei prodotti notevoli.
2)Il Teorema “di Pitagora” e quello “di Lazare Carnot”
3) La conseguente visualizzazione e scoperta dello Gnomone e della sua tecnica induttiva contenuta.
4) Il rapporto Aureo.
5) I primi concetti di Equivalenza, di Limite e Infinito.
6)La soluzione dei Problemi di 1°, 2° e 3° grado.
7)L’origine e lo sviluppo dei Poligoni e dei Poliedri regolari.”
Ciao Annarita, grazie ancora per avermi coraggiosamente appoggiato la pubblicazione di questa importante ricerca sulle origini del nostro pensiero algebrico prescientifico.
Aldo"