Il criterio di divisibilità per 11, come
il criterio di divisibilità per 7, è sicuramente uno di quelli meno immediati quanto a semplicità d'applicazione del proprio algoritmo; ciò nonostante, non si può fare a meno di conoscerlo, in quanto nell'ambito di una scomposizione in fattori primi si correrebbe il rischio di considerare primo un numero in realtà divisibile per 11. L'enunciato è il seguente:
un numero è divisibile per 11 se la differenza (in valore assoluto) tra la somma delle sue cifre che occupano posto pari e la somma delle cifre che occupano posto dispari dà come risultato un numero divisibile per 11. Il criterio è in realtà più semplice da applicare che da enunciare e basterà un esempio per capirlo.
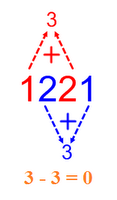
Vediamo come verificare che 1221 è divisibile per 11.Sommiamo le cifre che occupano posto pari, ossia quelle evidenziate in blu nell'immagine accanto; sommiamo le cifre che occupano posto dispari, cioè quelle evidenziate in rosso nella stessa immagine; ottenute le due somme, in tal caso entrambe pari a 3, eseguiamo la differenza in valore assoluto tra somma di cifre pari e somma di cifre dispari |3 - 3| = 0; 0 è multiplo di 11, quindi l'intero numero 1221 è divisibile per 11.
Per chi non sa cos'è il valore assoluto (è raro che lo si accenni al primo anno di scuola media), si può anche più semplicemente dire che non è importante l'ordine in cui si sottraggono le due somme; l'importante è che la somma eventualmente maggiore sia il minuendo, mentre la somma minore il sottraendo (esempio: se prendo come numero 39871, sommo le cifre di posto pari 9 + 7 = 16; sommo le cifre di posto dispari 3 + 8 + 1 = 12; non avrebbe senso ai nostri scopi 12 - 16, quindi eseguiamo 16 - 12). Il procedimento in sè non è difficile; bisogna soltanto fare attenzione all'enunciato, perché
bisogna sommare le cifre che occupano posti pari/dispari, non le cifre pari/dispari! Questo è infatti un errore comunemente commesso dagli studenti di prima media, soprattutto le prime volte in cui si va ad applicare il criterio.
Il criterio di divisibilità per 11, come il criterio di divisibilità per 7, è sicuramente uno di quelli meno immediati quanto a semplicità d'applicazione del proprio algoritmo; ciò nonostante, non si può fare a meno di conoscerlo, in quanto nell'ambito di una scomposizione in fattori primi si correrebbe il rischio di considerare primo un numero in realtà divisibile per 11. L'enunciato è il seguente: un numero è divisibile per 11 se la differenza (in valore assoluto) tra la somma delle sue cifre che occupano posto pari e la somma delle cifre che occupano posto dispari dà come risultato un numero divisibile per 11. Il criterio è in realtà più semplice da applicare che da enunciare e basterà un esempio per capirlo. Vediamo come verificare che 1221 è divisibile per 11.Sommiamo le cifre che occupano posto pari, ossia quelle evidenziate in blu nell'immagine accanto; sommiamo le cifre che occupano posto dispari, cioè quelle evidenziate in rosso nella stessa immagine; ottenute le due somme, in tal caso entrambe pari a 3, eseguiamo la differenza in valore assoluto tra somma di cifre pari e somma di cifre dispari |3 - 3| = 0; 0 è multiplo di 11, quindi l'intero numero 1221 è divisibile per 11.
Per chi non sa cos'è il valore assoluto (è raro che lo si accenni al primo anno di scuola media), si può anche più semplicemente dire che non è importante l'ordine in cui si sottraggono le due somme; l'importante è che la somma eventualmente maggiore sia il minuendo, mentre la somma minore il sottraendo (esempio: se prendo come numero 39871, sommo le cifre di posto pari 9 + 7 = 16; sommo le cifre di posto dispari 3 + 8 + 1 = 12; non avrebbe senso ai nostri scopi 12 - 16, quindi eseguiamo 16 - 12). Il procedimento in sè non è difficile; bisogna soltanto fare attenzione all'enunciato, perché bisogna sommare le cifre che occupano posti pari/dispari, non le cifre pari/dispari! Questo è infatti un errore comunemente commesso dagli studenti di prima media, soprattutto le prime volte in cui si va ad applicare il criterio.
Pacman
Nostradamus
Magical Cat Adventure
Snake