Il criterio di divisibilità per 7: il mistero di un'inspiegabile sparizione

Il mondo matematico è da anni terribilmente in ansia per il caso di una misteriosa ed inspiegabile scomparsa. E' un caso che anche "Chi l'ha visto?" potrebbe trattare, perché lascia veramente esterrefatti e con il patema d'animo che quella sparizione stia a significare una morte avvenuta con inesorabile gradualità nell'indifferenza comune. Fino ad ora tutti i libri di testo di matematica sono stati setacciati a fondo, ma nessuna traccia di esso; tanti insegnanti di matematica sono stati interpellati, ma i pochi che lo conoscono l'hanno definito un soggetto difficile da tenere a bada. E' giunto il momento di sguinzagliare i cani aritmetici per ritrovare il protagonista di questa sparizione e cercare di ridargli dignità ed orgoglio affinché non abbandoni di nuovo il mondo che gli ha dato la vita. Di chi, o meglio cosa, stiamo parlando?Il "siparietto" introduttivo di questo post ha come protagonista il criterio di divisibilità per il numero naturale 7. Sin da quando ho studiato a scuola, fino ad arrivare alla conclusione dei miei studi (SSIS inclusa), non ho mai trovato scritta in un libro di testo la regola per capire se un numero sia o meno divisibile per 7, nè colleghi studenti o insegnanti hanno mai saputo spiegarmela.
Così ad un certo punto ho deciso di cercarla in Internet e l'ho trovata! In pratica il criterio prevede che, se la differenza tra l'intero numero, letto senza la cifra delle unità, e il doppio dell'unità stessa, è un multiplo di 7, allora il numero è divisibile per 7. Troppo complicato? Naaa, è solo impressione. ^__^
Facciamo qualche esempio, considerando due numeri come 147 e 91.
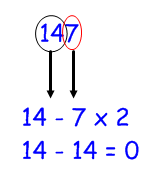1) Prendiamo in considerazione 147 privato della sola cifra delle unità: 14. 2) A 14 sottraiamo il doppio delle unità, ossia 2*7 = 14, ed avremo:14 - 14 = 0. 3) 0 è un multiplo di 7, allora 147 è divisibile per 7.Ripetiamo il procedimento anche con 91:
1) 91 privato dell'unità è 9. 2) Ad esso sottraiamo il doppio dell'unità, ossia 1*2 = 2, ed avremo: 9 - 2 = 7. 3) 7 è un multiplo di 7, allora 91 è divisibile per 7.Molte persone affermano che il criterio di divisibilità per 7 sia poco diffuso sui libri di testo perché meno utilizzato rispetto ad altri e, pertanto, non prioritario da apprendere. Il discorso può avere una sua logica, perché d'altronde lo stesso ragionamento si potrebbe fare per il criterio di divisibilità per 13, che sicuramente conosceranno ancora meno persone, e così via andando avanti. Qualcun altro afferma che esso è poco pratico da insegnare perché è elaborato il procedimento da svolgere, ma io in effetti dopo averlo sperimentato a scuola da alcuni anni, trovo che per gli alunni sia molto più difficile ricordare il criterio di divisibilità per 11, che invece è presente in tutti i libri in bella mostra!
Credo sia importante anche un'altra considerazione: un libro di testo non può assolutamente riportare il criterio di divisibilità per 4, per 6, per 8, per 9, per 10, per 25 e 100, saltando spudoratamente quello del 7! Se ad esempio ci si trova davanti ad un multiplo di 25 in una frazione da ridurre ai minimi termini, si arriverà comunque a semplificare la frazione, dividendo due volte per 5 anziché una sola per 25, per cui io potrei anche fare a meno di sapere il criterio di divisibilità per 25.Come si fa però quando si hanno davanti numeri come 91? Chiedete ad un qualsiasi alunno di scuola media (o anche superiore) se 91 sia numero primo. Vi risponderà senza dubbio di sì, perché "tanto non è divisibile per 2, nè per 3, nè per 5, nè per 11... Allora è primo!".Credo che molti libri di testo guadagnerebbero in qualità se eliminassero il superfluo privilegiando la coerenza.E chissà che, con essi, non migliori anche la qualità dell'insegnamento di alcuni concetti ^__^.