Impara a Programmare, Articolo Bonus 1: La Teoria delle Code

La Teoria delle Code

Quando la domanda e/o la capacita’ di erogazione di un servizio sono soggette ad aleatorieta’, si possono verificare situazioni in cui chi fornisce il servizio non ha la possibilita’ di soddisfare immediatamente le richieste.

La teoria delle code è lo studio matematico delle linee di attesa (o code) e di vari processi correlati, come l’arrivo alla fine di una coda, l’attesa (essenzialmente un processo di immagazzinamento) e l’essere servito all’inizio della coda. Tale teoria può essere applicata nei trasporti e nelle telecomunicazioni.

Una coda è costituita da uno o più “clienti” in attesa di un servizio da parte di uno o più “serventi”.

Un esempio di clienti: persone in attesa ad una cassa per una operazione bancaria, presse in attesa del montaggio di nuovi stampi.

Un esempio di corrispondenti serventi: l’impiegato alla cassa, gli addetti all’attrezzaggio del reparto presse.

Le code si formano a causa del non perfetto bilanciamento tra il ritmo con cui si manifesta la domanda del servizio ed il ritmo con cui il servente riesce ad elargirlo: questo è tanto più vero quanto più i tempi in esame risultano affetti da una certa aleatorietà, e non sono quindi impostati deterministicamente su valori prefissati (o, piu realisticamente, non è possibile farlo):

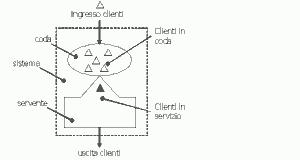
Figura 1: Modello generico di una coda

Struttura di un modello waiting line

Popolazione dei clienti: è la sorgente che genera gli input al sistema; se il numero potenziale dei nuovi clienti per il sistema è apprezzabilmente affetto dal numero di clienti già presenti internamente al sistema, la popolazione è detta finita. Alternativamente in una popolazione infinita il numero dei clienti nel sistema non influenza il ritmo con cui nuovi clienti richiedono il servizio.

Il servizio è descrivibile in funzione del numero di serventi s, e del numero di linee realizzate: single-line e multi-line (per la simbologia fare riferimento alla figura 1):

Figura 2: Modelli di coda single-line e multi-line

La regola di ordinamento delle coda (ranking rule) stabilisce quale sarà il prossimo cliente ad essere servito:

FIFO First In First Out
LIFO Last In First Out
EDD Erliest Due Date
SPT Shortest Processing Time

La sorgente di variabilità nei modelli waiting lines deriva dalla possibile casualità dei tempi di interarrivo dei clienti nel sistema, e dai tempi di effettuazione del servizio e si può dimostrare che se i clienti arrivano in modo completamente casuale ed indipendente tra di loro, è possibile descrivere la legge di arrivo tramite una distribuzione di Poisson [4]:

P(n)=(( lT)ⁿ/n!) e ^-^l^T con n = 1,2,…

dove:

P(n) probabilita di n arrivi nel periodo T
l numero medio di arrivi nell’unita di tempo
e numero di Eulero e = 2.7183

In generale, comunque siano esprimibili le distribuzioni dei tempi di interarrivo e quelle dei tempi di servizio, siano pure essi deterministici, indicheremo con l, sempre il valore atteso della frequenza di interarrivo, e con m il valore atteso della frequenza di servizio (risulterà allora che il tempo medio di interarrivo sarà pari a 1/l, ed il tempo medio di servizio pari a 1/m).

Riassumendo, possiamo quindi fare riferimento ai seguenti parametri:

l intensita degli arrivi [unita /tempo]
m intensita del servizio [unita /tempo]

1/l tempo medio tra un arrivo ed il successivo [tempo]
1/m durata media del servizio [tempo]

Da notare che, più che di medie, sarebbe corretto parlare di valori attesi, nel senso che si tratta dei valori più probabili attesi.

I sistemi modellizzabili come waiting lines possono essere rappresentati dai seguenti parametri, che risultano caratteristici al fine di poter esprimere il livello del servizio erogato, i costi del sistema e i coefficienti di utilizzo degli impianti con cui il servizio viene erogato:

L_q lunghezza della coda: è il numero di clienti presenti in coda in un certo istante
W_q tempo medio di attesa in coda: è il valore medio calcolato sui tempi di attesa in coda di ciascun cliente
L lunghezza della linea: è il numero di clienti presenti in coda in un certo istante più il numero dei clienti serviti in quell’istante.
W tempo medio di attesa nella linea: è il valore medio calcolato sui tempi totali di attesa e di servizio per ciascun cliente.
r=l/mc tasso di utilizzo del sistema: è il coefficiente che esprime il grado di utilizzazione del sistema, dove c rappresenta il numero dei serventi.

Notazione di Kendall

La notazione di Kendall risulta essere del tipo A/B/c/K/m/Z dove:

A identifica la distribuzione degli arrivi dei clienti
B identifica la distribuzione dei tempi di servizio
c identifica il numero dei serventi
K identifica la capacita del sistema (del buffer, default infinita)
m identifica la dimensione della popolazione (default infinita)
Z identifica la disciplina del servizio (default FIFO)

Generalmente la codifica si ferma alle prime tre componenti (esempio: M/G/1) in particolare, le lettere di uso comune da impiegare per la notazione sono:

M indica una distribuzione esponenziale negativa (Markoviana)
G una distribuzione Gaussiana
D una distribuzione costante (degenere)

inoltre:

P₀ indica la probabilità di non avere clienti in coda
P_n indica la probabilità di avere n clienti in coda

Influenza del fattore di utilizzazione r

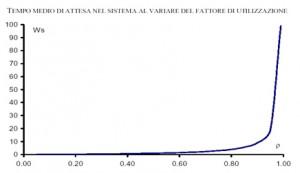
Figura 3: tempo medio di attesa in coda al variare di r

Come si desume dalla figura 3 al crescere di r aumenta conseguentemente l’occupazione del server e quindi la permanenza media ed il numero medio dei clienti in un sistema (come un cluster Grid), nonche` il numero medio ed il tempo medio dei clienti in attesa [4]. Ad un incremento di r dunque corrisponde una maggiore utilizzazione delle risorse disponibili. Viceversa, se l’aumento di r è dovuto all’utilizzo di server meno veloci, dovrebbero diminuire di conseguenza i costi di acquisizione degli stessi. In un problema di progetto di sistemi sarebbe dunque auspicabile tenere conto del fattore r, cercando un giusto compromesso tra costi, prestazioni (qualita`) ed utilizzazione delle risorse [4].

Un altro fattore molto importante che è influenzato da r è il tempo di raggiungimento del regime, ovvero il tempo dopo il quale le statistiche che descrivono il comportamento medio del sistema non variano piu` in modo significativo e quindi il processo che descrive la dinamica della coda puo` essere ritenuto praticamente stazionario.