Interpretazione cinematica dei punti angolosi: moto in un campo di Heaviside

I punti angolosi del grafico di una funzione reale di una variabile reale si prestano a una interessante interpretaziuone cinematica. Per essere più precisi, consideriamo una pallina che si muove in un piano di moto uniforme. Fino a un istante t₀ la traiettoria è una retta assegnata; a t₀ la pallina devia "istantaneamente" percorrendo un'altra retta con velocità costante, come mostrato nella fig. al top di questo post. In altri termini, in t₀ la velocità ha una discontinuità di prima specie: il suo modulo è costante, ma la direzione muta istantaneamente. Per quanto precede, la componente secondo l'asse y della velocità della pallina è:

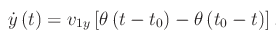
il cui grafico è:

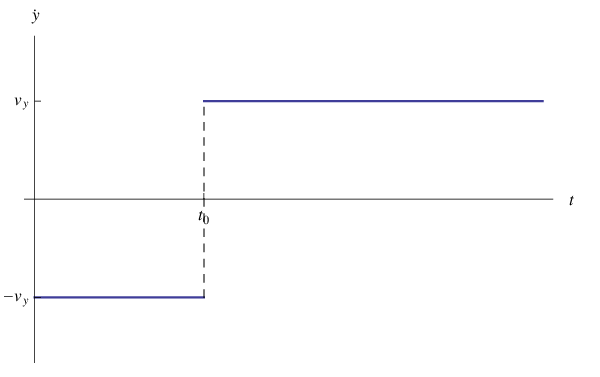
Osservando che la derivata della funzione di Heaviside è la delta di Dirac, si ha che la componente y dell'accelerazione è:

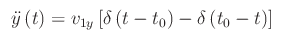
Se m è la massa della pallina, la forza agente su di essa è:

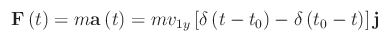
che espressa in funzione dell'ordinata y:

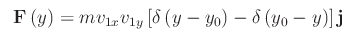
Abbiamo così trovato che la pallina è sottoposta a una forza posizionale e come tale derivabile da un'energia potenziale:

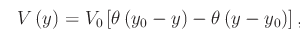
il cui grafico è:

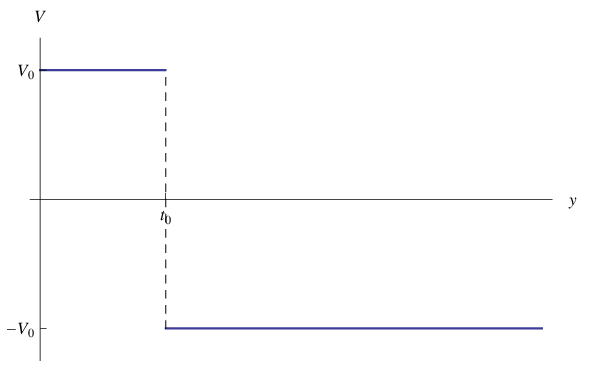
Ne consegue che l'energia potenziale V, e quindi il potenziale U=-V, si esprime attraverso una combinazione lineare di funzioni di Heaviside. Ciò suggerisce di chiamare la grandezza U potenziale di Heaviside

Ne concludiamo che una particella che si muove in un campo di Heaviside ha un'accelerazione deltiforme.

Per i dettagli matematici, consultare il seguente file pdf:
campo_heaviside.pdf