L'evoluzione per sottrazione

Una delle teorie maggiormente sostenute dai detrattori dell'evoluzionismo consiste nel pensare che l'evoluzione non avvenga per aggiunta graduale di nuove caratteristiche, come si è sempre detto, perché le strutture biologiche molto complesse, come il nostro occhio ad esempio, hanno un grado di organizzazione troppo elevato per poter spiegare che ciascuna parte anatomica si sia aggiunta pezzo dopo pezzo alle precedenti col passare del tempo. Proviamo ad immaginare il nostro occhio senza retina oppure senza cristallino: funzionerebbe nella stessa maniera? Ovviamente no, ma è anche vero che esistono esempi di occhi rudimentali presenti in animali meno complessi che, anche se organizzati in maniera diversa dal nostro, svolgono tuttavia la loro funzione ugualmente bene.  Dunque fino ai giorni nostri si è sempre pensato che l'evoluzione procedesse per addizione di nuove caratteristiche alle precedenti, ma se invece in alcuni casi procedesse per sottrazione di caratteristiche comparse, provando a ribaltare questo paradigma? Potrebbe ad esempio essere che in natura, in determinati momenti dell'evoluzione, compaiano organi o tessuti già complessi, magari così tanto da non funzionare  subito egregiamente, e che poi via via col passare del tempo si affinino sempre più e si organizzino sempre meglio eliminando il superfluo? E' così che i ricercatori Dan McShea e Wim Hordjik, in uno studio recentemente pubblicato sulla rivista Evolutionary Biology, hanno proposto un nuovo modello interpretativo dell'evoluzione, chiamato "evoluzione per sottrazione". Anziché cominciare da strutture semplici che diventano più complesse per aggiunta di nuove parti nel corso del tempo, secondo i ricercatori non è impensabile ragionare al contrario, ossia immaginare che determinate strutture compaiano già "grezzamente complesse", grazie ad un certo assetto genetico, e che via via si semplifichino eliminando le parti o le funzionalità superflue o poco efficienti. 

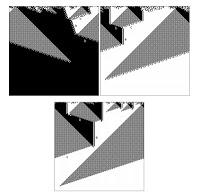
In questi grafici l'asse delle ascisse rappresenta
le unità disposte nello spazio l'una accanto all'altra;
l'asse delle ordinate rappresenta il tempo, che aumenta
dall'alto verso il basso

Per testare quest'idea, gli studiosi hanno sfruttato un complesso modello matematico con simulazione virtuale di evoluzione, in cui le strutture anatomiche complesse sono rappresentate da una fila orizzontale di cellule (chiamati cellular automata), a loro volta raffigurate da quadratini neri o bianchi, come i quadrati di una scacchiera. In tale modello computerizzato, i quadratini possono cambiare colore da bianco a nero e viceversa, in base ad un certo set di regole che imitano i trend naturali dell'ereditarietà, mutazione, ricombinazione e riproduzione. A seconda di quanto bene le "unità cellulari" rispondono ad un certo input o ad un compito assegnato, può cambiare il set di colore bianco-nero in un certo modo, e le unità acquistano una certa probabilità di passare alla generazione successiva e portare a quest'ultima il set di cambiamenti eventualmente ereditato, con cui hanno risposto ai compiti dati. I ricercatori hanno osservato che i pattern iniziali di colori erano molto complessi, ma di generazione in generazione alcune regole di disposizione delle unità hanno prodotto associazioni più semplici e lineari, e le unità sono diventate più efficienti nello svolgere i compiti successivamente assegnati. Gli studiosi sono convinti che tale modello possa rappresentare bene quello che in natura accade e già potrebbe essere accaduto diverse volte, senza sostituire la tradizionale teoria evolutiva "per addizione", bensì
affiancandosi a questa in parallelo, come ulteriore ipotesi di scenario evolutivo. Basti pensare ad esempio a quanto complesso era il cranio di alcuni pesci primitivi (es. i placodermi) e a quanto si sia semplificata l'organizzazione dello stesso a partire dai primi pesci fino ad arrivare al genere Homo.

I placodermi, gruppo di pesci estinto

Evoluzione del cranio da pesci primitivi al genere Homo

McShea, D., & Hordijk, W. (2013). Complexity by Subtraction Evolutionary Biology DOI: 10.1007/s11692-013-9227-6