[¯|¯] La costante di Feigenbaum, la costante di struttura fine e l'età dell'Universo

Sto leggendo Se questo è l'infinito del fisico Emilio Santoro.

Sono ancora all'"inizio", considerando la lunghezza del libro (oltre 700 pagine). Ieri sera, navigando nell'indice ho trovato un capitolo interessante (al di là dell'impianto narrativo, di per sé eccellente). Il protagonista, "quasi" l'alter ego dell'autore (per esigenze narrative), è un astrofisico che si imbatte in uno strano legame tra la costante di Feigenbaum, la costante di struttura fine, pi greco e l'età dell'universo. Tale legame è solo l'inizio di una teoria elaborata dall'autore e che si sviluppa nelle pagine successive, e che tuttavia ha suscitato il mio interesse, poichè in un vecchio articolo avevo trattato la mappa logistica in ambiente Mathematica. L'articolo può essere letto a questo link (pagg. 61 e s.), la cui idea di partenza è che la mappa logistica altro non è che un'equazione differenziale del tipo Bernoulli-Riccati che regola l'evoluzione di un sistema dinamico a tempo continuo, scritta "nel tempo discreto" (per essere più precisi, si tratta di un automa cellulare). Incidentalmente, un sistema a tempo continuo governato da un'equazione del tipo Bernoulli-Riccati non è caotico (pur essendo non lineare). Ne consegue che il caos deterministico non è di origine fisica, ma computazionale. In tal modo l'esistenza in natura del caos deterministico non farebbe altro che corroborare l'interpretazione pitagorica dell'universo (in forza dell'origine computazionale, quindi numerica del caos).

Per concludere questo post "approssimativo", ricordiamo brevemente come esce fuori la costante di Feigenbaum. La mappa logistica è un sistema dinamico iterato con funzione di trasferimento:

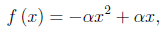
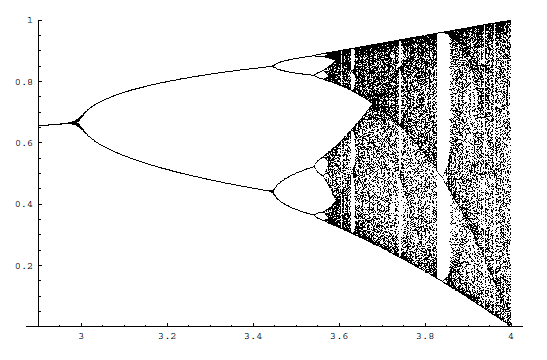
dove "alpha" è un parametro reale positivo. Esistono valori caratteristici di tale parametro. Ad esempio, per alpha compreso tra 1 e 3, il diagramma delle orbite presenta un solo punto fisso (attrattore stabile). Per alpha=3 si verifica un raddoppiamento del periodo, nel senso che lo stato del sistema oscilla tra 2 attrattori stabili. Per alpha=3.45 abbiamo un nuovo raddoppiamento del periodo e così via per altri valori caratteristici. Esiste un valore caratteristico per il quale ogni punto è un attrattore. Il sistema diviene dunque caotico. Viene poi definita la successione:

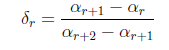
E quindi la costante di Feigenbaum: