Negli appunti di oggi trattiamo la funzione esponenziale nel campo complesso (in riferimento alla precedenti lezioni sulle funzioni olomorfe). Il nostro punto di partenza è la dimostrazione della formula:
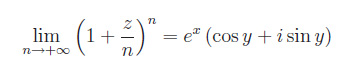
che suggerisce la seguente definizione:
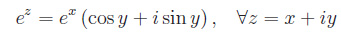
La funzione esponenziale è olomorfa su tutto il piano complesso.
Per dimostrarlo basta applicare il teorema dimostrato nella suddetta lezione, secondo cui condizione necessaria e sufficiente affinchè una funzione complessa sia olomorfa in un campo A, e che essa sia ivi differenziabile secondo Stolz e che soddisfi le equazioni di Cauchy-Riemann (nel campo A).
Pacman
Nostradamus
Magical Cat Adventure
Snake