La spiegazione scientifica del perché il monobraccio è un'aberrazione meccanica

Il nostro amico Marc poels ha chiesto ad un suo amico ingegnere cosa ne pensava dei forcelloni monobraccio, e gentimente mi ha girato la sua interessante risposta, inclusi i preziosi schizzi che rendono chiaro quello che spiega.
Lo riporto in francese e in una pessima traduzione in Italiano:
Le monobras est effectivement moins performant sur le strict plan mécanique. Un simple schéma tel que ci-dessous met en évidence que, pour une même sollicitation mécanique transmise par le bras oscillant, le monobras aura fort à faire (en pointillé, les allures des déformées respectives de chaque type de bras.
Il monobraccio è in realtà meno efficiente da un punto di vista strettamente meccanico. Uno schema semplice, come di seguito mostra che, per lo stesso stress meccanico trasmesso dal forcellone, il braccio singolo ha molto a che fare (linea tratteggiata, le forme deformi rispettivi bracci di ogni tipo.

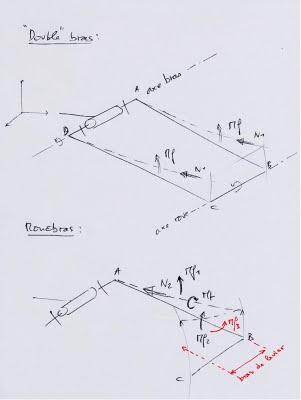
- chaque branche du bras classique (double branche) transmet un moment fléchissant Mf (maximal à l'ancrage sur le cadre (ou le moteur ;) ), et un effort normal de compression (dû à la force motrice) N1.
- l'unique branche du monobras transmet un moment fléchissant Mf1 (= 2 x Mf) et un moment de torsion Mt , en plus d'un effort normal de compression N2 (= 2x N1). De plus, l'axe de roue transmet un moment fléchissant Mf2 Chaque architecture étant soumise à un même chargement, on peut déterminer les contraintes mécaniques au point A si l'on connaît les dimensions des sections qui constituent les bras, aux points A respectifs de chaque structure. Rque : mon raisonnement est simplifié, je ne considère notamment pas l'action de la suspension (qui complique les choses mais ne change rien au final : le monobras sera terrassé).
Pour la démonstration, je vais considérer (au départ) que chacune des branches (AB et CD pour le bras classique, AB pour le monobras) est constituée d'un même tube de section circulaire pleine de diamètre D ( c'est pour simplifier, mais les résultats sont absolument transposables à des sections annulaires, rectangulaires pleines ou creuses, etc.). Chaque tube sera constitué d'un même matériau (mettons de l'acier, mais tout matériau élastique et isotrope ferait l'affaire) dont les caractéristiques mécaniques utiles seront : - le module de Young E, (module d'élasticité, souvent exprimé en gigapascals GPa, = environ 210 GPa pour de l'acier) - le coefficient de Poisson n (sans unité, = environ 0,3 pour de l'acier) - la masse volumique mv (en kg/m3, = environ 7800 kg/m3 pour de l'acier)
Peu importent les valeurs réelles des contraintes que je vais calculer, seuls comptent les faits suivants : pour une pièce constituée du même matériau, la rupture (ou la déformation plastique) interviendra pour un même état de contrainte. L'état de contrainte d'une pièce, en un point de sa section, ne dépend que de l'effort qu'elle transmet et de ses dimensions.
Mon but est de montrer qu'à chargement égal, au niveau de la roue : - soit le monobras doit être plus lourd pour être aussi rigide, - soit le monobras est moins rigide à masse égale.
Dans un premier temps, je ne tiendrai compte que des contraintes dites normales (dues aux moments de flexion et à la compression).

- Ogni braccio di forcelloni convenzionali (due gambe) trasmette un momento flettente Mf (massima all' ancoraggio sul telaio (o motore;)), e una forza normale di compressione (a causa della forza motrice) N1.
- L'unica sezione resistente di un monobraccio trasmette il ​​momento flettente MF1 (= 2 x Mf) e un momento torcente Mt, oltre ad una forza normale di compressione N2 (N1 = 2x). Inoltre, l'asse della ruota trasmette un momento flettente MF2 .
Sottoponendo ogni architettura allo stesso carico, possiamo determinare le sollecitazioni meccaniche nel punto A se conosciamo le dimensioni delle sezioni resistenti dei rispettivi punti A di ciascuna struttura.
E: Il mio ragionamento è semplice, non ritengo che tale tipo di sospensione (che complica le cose, ma non porta vantaggi finali: il monobraccio è perdente).
Per la dimostrazione, si assumerà (inizialmente) che ciascuno dei comparti (AB e CD per il braccio classico, AB per il monobraccio) sia costituito da un unico tubo di solida sezione circolare di diametro D (che per semplicità, ma i risultati sono assolutamente trasferibili alle sezioni rettangolari pieni o cavi, ecc) .. Ogni tubo è fatto dello stesso materiale (ad esempio l'acciaio, ma qualsiasi materiale isotropo elastico e idoneo) le cui caratteristiche meccaniche sono utili:
- Il modulo di Young E (modulo di elasticità, spesso espresso in gigapascals GPa, = 210 GPa per l'acciaio)
- N rapporto di Poisson (adimensionale, = circa 0,3 per l'acciaio)
- Mv densità (in kg/m3 = 7.800 kg/m3 per l'acciaio)
Indipendentemente dai valori effettivi dei vincoli che vado a calcolare, contano solo i seguenti fatti: per un pezzo dello stesso materiale, frattura (o deformazione plastica) si verifica per lo stesso livello di sollecitazioni o stress. Lo stato di stress di una struttura, ad un certo punto della sua sezione, dipende solo dallo sforzo in rapporto con le sue dimensioni.
Il mio obiettivo è quello di mostrare che a parità di carico :
- Il monobraccio deve essere più pesante per essere ugualmente rigido
- Il monobraccio è meno rigido a parità di massa.
In un primo momento, mi limito a prendere in considerazione le cosiddette normali sollecitazioni (causate da momenti di flessione e compressione).

AscoltaTrascrizione fonetica

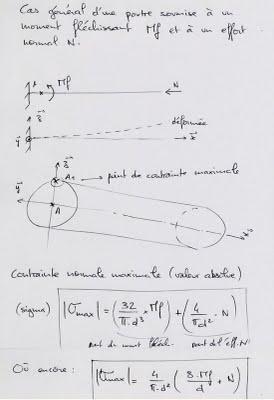
Si l'on s'en tient aux sollicitations immédiatement "perceptibles" flexion et compression, il suffit d'une seule branche pour faire le travail de deux, à la condition que la branche unique soit de dimensions compatibles avec cette double sollicitation. La résistance à la flexion étant liée au diamètre au cube, la résistance à la compression étant liée au carré du diamètre, on ne peut pas calculer l'inflation nécessaire de la section si on ne connaît pas le rapport précis entre l'effort de compression N (lié à la force motrice) et le moment fléchissant (lié à la longueur du bras et à l'effort normal du contact roue/sol qui dépend de la masse, de sa répartition initiale et de la valeur de l'accélération instantanée - mais la théorie des poutres que j'utilise ici n'est théoriquement valide que dans les cas statiques).
A ce stade, imaginons que les dimensions du monobras croissent d'un facteur (racine de 2) pour obtenir un état de contrainte équivalente (donc une résistance équivalente à matériau donné). Alors la section voit son aire augmenter d'un rapport 2. La masse linéique est donc doublée.
A ce stade toujours, on pourrait conclure qu'une branche unique qui a la même masse que deux branches dédoublées offre les mêmes performances mécaniques.
OUI MAIS NON. Car je n'ai pas encore comptabilisé les effets des moments de torsion. L'ajout de la sollicitation de torsion conduit à l'expression d'une contrainte de cisaillement, maximale au même point. Or le monobras est soumis à un moment de torsion, important, au point A. L'honnêteté intellectuelle me force à préciser que quelques moments de torsion seront bien créés, en pratique, dans le bras classique (pour cause de dissymétries diverses, par manque de rigidité de l'axe de roue, etc.), mais resteront toujours incomparablement plus faibles.
Or l'influence des contraintes de cisaillement sera nécessairement néfaste aux performances mécaniques de la structure. Peut-être avez-vous fait un peu de résistance des matériaux lors de vos études d'architecture, auquel cas vous connaissez peut-être quelques méthodes pour établir les états de contrainte dans le cas de sollicitations composées (cercles de Mohr ?). Sinon, il faut juste retenir que la méthode généralement la plus appropriée est une méthode appelée critère de Von Mises, qui fait calculer une "contrainte équivalente" à laquelle chaque contrainte contribuera.
La contrainte de cisaillement, due à la torsion, directement associée au monobras, fera ainsi augmenter l'état de contrainte au point déjà le plus sollicité. Pour compenser cela, il faudra rajouter de la matière ou changer le matériau pour un plus résistante, etc.
MAIS CE N'EST PAS TOUT ! Il reste la question du flambage. Le fait que l'effort normal, dû à la force motrice, ne soit pas appliqué (dans le cas du monobras) au niveau de la branche unique mais avec un décalage latéral, produit une forme de flambage, qui en l'occurrence serait plutôt une autre forme de flexion (Mf3), dans un plan perpendiculaire à la première flexion (Mf1). De toute façon, la combinaison compression + flexion n'a jamais fait bon ménage (ce n'est pas à un architecte que je l'apprendrai). A mon avis, c'est même là que se situe le problème majeur. Un problème encore plus crucial une fois que l'on passe en dynamique (mais il nous faudrait quelques mois de formation, au minimum pour en discuter sérieusement : c'est aujourd'hui traité de façon numérique, le plus souvent).
//////////////////////////////////////////////////////////////////////////////////////// Fin de la démonstration ////////////////////////////////////////////////////////////////////////////////////////
En résumé, c'est la torsion, inévitable dans le cas du monobras, qui, ajoutée au problème de flambage, interdit absolument d'espérer, à moyens égaux, de fabriquer un monobras aussi performant qu'un bras classique. Il y aura toujours quelqu'un pour raconter qu'avec une solide étude numérique, l'utilisation de matériaux encore plus nobles et de formes novatrices, il aura fabriqué le monobras aussi performant qu'un bras classique, mais il suffira de lui opposer qu'avec les mêmes moyens, on fabriquera un bras classique encore plus performant, et ainsi de suite.
Autres inconvénients inhérents au monobras :

• la réalisation de roues elles aussi modifiées pour transmettre des efforts supplémentaires par rapport au cas du bras classique. Pour les mêmes raisons et sans entrer dans le détail, elles seront plus lourdes,
• l'intégration de nombreuses fonctions qui conduit à surdimensionner les parties assurant les interfaces avec le cadre (passage de la chaîne) et avec la roue (couronne et disque de frein du même côté),
• enfin, toutes ces contraintes mécaniques supplémentaires jouent leur rôle en terme de fatigue, c'est une sorte de cercle vicieux.

De toute façon, il me semble bien que le monobras a initialement été utilisé en course uniquement pour l'endurance (ELF, il me semble !?). Pour ce que j'en sais, Honda l'a ensuite repris sur ses machines de route (et BM, avec beaucoup d'intelligence, car cette solution se marie très bien avec la transmission par arbre). Que Ducati ait équipé sa sublime 916 de cet accessoire n'est-il pas qu'un coup de frime ? Est-ce un hasard de l'avoir retrouvé ensuite sur la MV F4 (entre autres caractéristiques "stylistiques" communes bien compréhensibles...) ?
Et puis il y a l'argument de la réalité pratique : quelle MotoGP utilise un monobras ? Pourquoi les japonais n'ont-ils jamais cédé au monobras sur leurs hypersport (NR 750 exceptée, mais le propos de cette machine n'a jamais été le sport, soyons raisonnables. Tiens, encore une moto avec des pots sous la selle...) Pourquoi Terreblanche a-t-il couru le risque (et en a-t-il payé les conséquences) de se couper des afficionados de Ducati en revenant au bras classique sur la 999 ? Je l'aimais bien, moi, Terreblanche : la 999 était un exemple de conception intelligente, du vrai DESIGN, qui laissait de côté les préoccupations esthétiques.
916, 999, 1098, MV F4, NR 750. Qu'avaient-ils tous à vouloir coller les pots sous la selle sur des 4T ? Voilà une autre sorte d'aberration du point de vue des performances mécaniques... Prochain sujet de conversation ?

Se ci atteniamo alle esigenze immediatamente "visibili" flessione e compressione, può essere sufficiente un solo braccio per fare il lavoro di due a condizione che sia di sezione sufficiente. La resistenza alla flessione è legata al cubo diametro, la resistenza alla compressione è legata al quadrato del diametro, non possiamo calcolare sezione richiesta se non si conosce l'esatta relazione tra laforza di compressione N (legato alla forza motrice) e momento flettente (a causa della lunghezza del braccio e la forza normale del contatto ruota/suolo dipende dalla massa, la sua ripartizione iniziale, e il valore della accelerazione istantanea - ma la teoria dei travi che uso qui è teoricamente valida solo per un calcolo statico statico).
A questo punto, immaginare che le dimensioni del monobraccio crescano di un fattore (√ 2) per ottenere un equivalente stato di stress (cioè una resistenza equivalente a parità di materiale). Mentre la sezione viene aumentata di 2 volte. La densità lineare è raddoppiato.
In quella fase, si potrebbe ancora concludere che un singolo braccio che ha la stessa massa della somma di 2 bracci possa offrire le stesse prestazioni meccaniche.
SI 'MA NO. Perché io non ho ancora preso in considerazione gli effetti dei momenti torsionali. L'aggiunta di stress torsionali conduce all'espressione di un massimo sforzo di taglio nello stesso punto. Tuttavia, il braccio singolo è sottoposto a torsione importante al punto A. L' onestà intellettuale mi costringe a chiarire alcuni momenti flettenti rimangono anche nella soluzione convenzionale (a causa di asimmetrie varie, la mancanza di rigidità del perno ruota, ecc.), ma sarànno sempre incomparabilmente inferiori.
Anche la sollecitazione a taglio è dannosa per le prestazioni meccaniche della struttura. Forse hai fatto un po 'di resistenza dei materiali durante gli studi in architettura, nel qual caso si può conoscere alcuni metodi per determinare lo stato di stress (cerchi di Mohr?). In caso contrario, basta ricordare che il metodo più appropriato è in genere un metodo chiamato criterio Von Mises, che calcola uno "stress equivalente" alla quale ogni vincolo contribuisce.
Le sollecitazioni a taglio causate dalle torsioni direttamente connessi con un solo lato, aumenta lo stato di stress nel punto più sollecitato. Per compensare questo, si aggiunge del materiale o si modifica il materiale per aumentare la resistenza, ecc.
Ma non è TUTTO! Resta la questione di instabilità. Il fatto che la forza normale causata dalla forza motrice non viene applicata centralmente (nel caso del monobraccio) , ma con uno spostamento laterale, produce una forma di deformazione, che in questo caso sarebbe piuttosto un'altra forma di flessione (MF3), su un piano perpendicolare alla prima flessione (MF1). In ogni caso, la combinazione di compressione + flessione non è mai andato bene insieme (non è una cosa che voglio insegnare ad un architetto). A mio parere, è ancora lì che sta il problema principale. Un fattore ancora più importante una volta che analiziamo la situazione in movimento (ma avremmo bisogno di alcuni mesi di formazione, almeno per discuterne sul serio: e di trasferire tutto in digitale).
////////////////////////////////////////////////// //////////////////////////////////////
Fine della dimostrazione.
////////////////////////////////////////////////// //////////////////////////////////////
In sintesi, la torsione è inevitabile nel caso di un singolo braccio, che aggiunto al problema della instabilità, annulla la speranza dei progettisti di raggiungere la parità di efficienza fra monobraccio e tradizionale. C'è sempre qualcuno che dice che un grande studio matematico e l'utilizzo di materiali migliori porterà alla parità di efficenza, ma ci sono abbastanza informazioni per dire che con le stesse capacità progettuali e gli stessi materiali si potrà sempre fare un forcellone tradizionale migliore di un monobraccio, e così via...
Altri svantaggi inerenti al braccio singolo:
Le ruote da usare con il monobraccio per raggiungere le stesse caratteristiche di robustezza ed affidabilità dovranno per forza essere più pesanti. L'integrazione di numerose funzioni porta a sovradimensionare le parti che forniscono le interfacce con il telaio (dalla catena) e con la ruota (corona e freno a disco sullo stesso lato) .
Infine, tutte queste ulteriori sollecitazioni meccaniche svolgono il loro ruolo in termini di affaticamento (dei materiali), una sorta di circolo vizioso.
Comunque, mi sembra che il braccio singolo è stato originariamente utilizzato solo per la gara di resistenza (ELF, credo!?). Per quanto ne so, la Hondalo ha poi ripreso su macchine stradali (e BMW, con molta intelligenza, in quanto questa soluzione va molto bene con l'albero di trasmissione). Ducati ha dotato la sua sublime 916 con questo accessorio, non è un colpo da maestro? E 'una coincidenza di aver trovato poi la MV F4 (tra le altre caratteristiche "stilistiche" comune comprensibile ...)?
E poi c'è l'argomento della realtà pratica: MotoGP utilizza monobraccio? Perché i giapponesi che l'hanno creato non hanno mai ceduto alla tentazione di usarlo sulle loro ipersportive ?(NR 750 escluso, ma su questa macchina non è mai stato lo sport il traguardo previsto. Perché, anche una moto con marmitte sotto la sella ...) Terreblanche Perché ha rischiato (e ha pagato le conseguenze) portare gli appassionati di Ducati al ritorno alle armi convenzionali sulla 999? A me il lavoro di Terreblanche è piaciuto: la 999 è stata un esempio di disegno intelligente, DESIGN reale, lasciando da parte le preoccupazioni estetiche.
916, 999, 1098, MV F4, NR 750. Che cosa hanno fatto! Tutti vogliono attaccare gli scarichi sotto la sella sui 4T? Questo è un altro tipo di aberrazione in termini di prestazioni meccaniche ... Prossimo argomento di conversazione?

Fabien AUDRY