Nel post precedente abbiamo illustrato tramite animazione grafica, la definzione di limite di una funzione reale di una variabile reale.
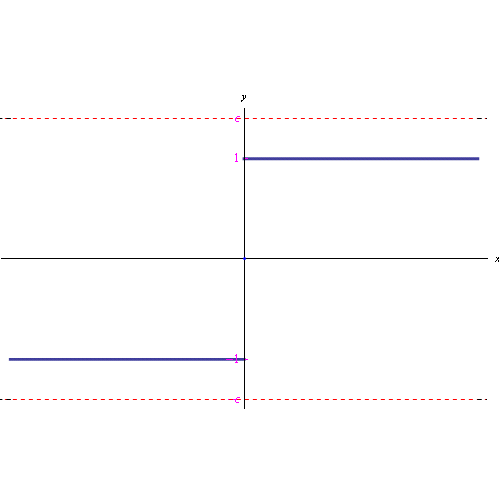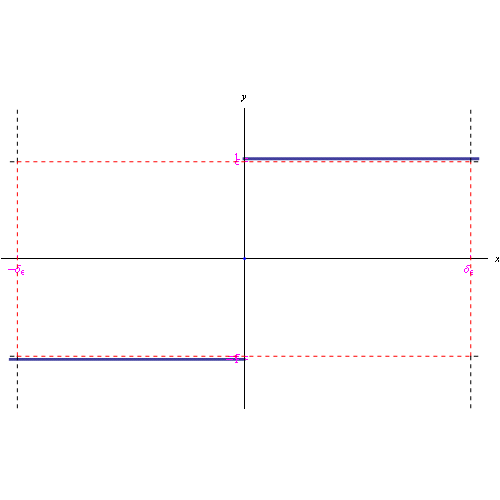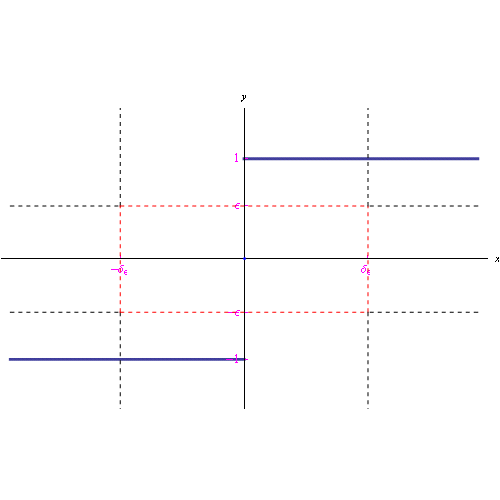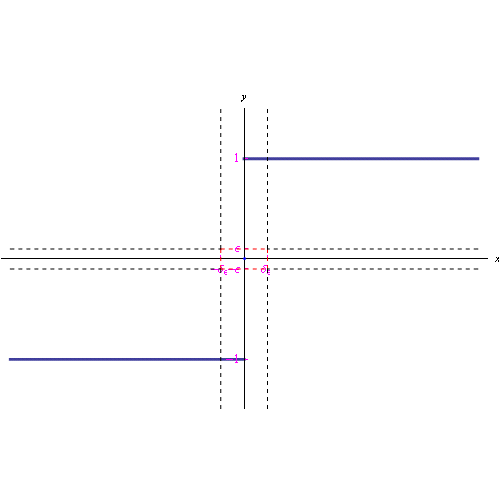
Oggi esaminiamo il caso di una funzione non regolare in un punto di accumulazione (al finito) del suo campo di esistenza. Più precisamente, consideriamo la funzione signum. Tale funzione è non regolare in x=0. Infatti supponendo che il limite sia zero, deve essere (con ovvio significato dei simboli):
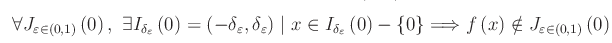
Cioè, comunque prendiamo un intorno J del punto f(0)=0, possiamo associare ad esso intorni I di x=0 tali che per ogni x appartenente ad I e distinto da x0=0, i punti f(x) non appartengono a J, come illustrato dalla figura seguente.

A una conclusione analoga si giunge se proviamo ponendo lim=1 o -1. Ne consegue che la funzione signum non è regolare in x=0, pur essendo ivi definita. Vedremo in seguito, che è regolare "a sinistra" e "a destra".
