Limite di funzioni ricorsive. Frattalità

L'argomento di questo post tratta un'idea nata da una conversazione sul gruppo Matematica di Facebook.
Assegnata la funzione

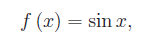
abbiamo visto che denotando con f_n(x) la composizione n-esima di f(x) con se stessa:

si ha:

dove:

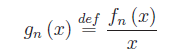
Ci poniamo ora il seguente problema:

Problema
Qual è il comportamento di g_n(x) per x->0 se il numero n delle iterazioni tende a +oo?

Iniziamo con l'osservare che l'intero naturale n svolge il ruolo di parametro, nel senso che per un assegnato n (eventualmente per n->+oo), noi studiamo il comportamento di g_n(x) nel limite per x->0. Da un punto di vista formale, possiamo tentare di risolvere il problema proposto assumendo n come variabile indipendente, considerare cioè la funzione reale g(x,n) definita in A:

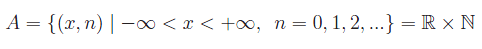
per poi eseguire l'operazione di passaggio al limite:

Più precisamente, assumiamo

ad esempio:

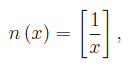
dove [.] denota la parte intera di un numero reale. Quindi abbiamo il seguente limite:

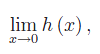
dove:

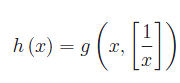
Abbiamo già studiato la funzione [1/x] in questa dispensa. Inoltre, rinunciando al tentativo di risolvere analiticamente il problema posto, proviamo con l'approccio computazionale, ottenendo il grafico:

Da tale grafico vediamo che il limite di h(x) vale 1. Tuttavia in ogni intorno di x=0, ci sono infiniti punti di discontinuità di prima specie. Ne consegue che la funzione h(x) non è generalmente continua, anzi non è nemmeno una funzione nel senso ordinario del termine.

Scarica l'articolo in formato pdf