La nozione di limite di una funzione reale di una variabile reale è di fondamentale importanza in analisi matematica. Incidentalmente, è possibile definire il concetto di derivata e di integrale definito proprio grazie all'operazione di passaggio al limite. Al tempo stesso, tale nozione è la più ostica, in quanto non esiste una regola generale per il calcolo dei limiti a differenza di ciò che avviene nel caso delle derivate.
Inoltre, l'utilizzo del sistema di computer algebra Mathematica permette di determinare i limiti di funzioni "molto complicate". Osserviamo, tuttavia, che trattandosi di un software, va utilizzato nel giusto modo. È chiaro che Mathematica fornisce solo il risultato finale, e di per sé questo è già molto, in quanto ci permette di controllare i risultati. Inoltre, grazie ad alcuni comandi di manipolazione di espressioni analitiche, è possibile verificare la correttezza dei passaggi intermedi finalizzati alla rimozione delle forme indeterminate.
Ciò premesso, esaminiamo una semplice routine che ci permette di calcolare i limiti di funzioni razionali fratte. Qui la forma indeterminata è 0/0. Il comando è il seguente:
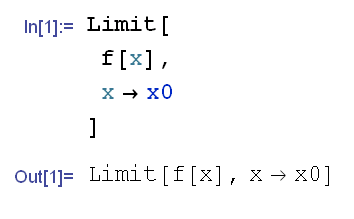
Ovviamente Mathematica restituisce l'input, poichè non conosce nè l'espressione della funzione nè il valore di x0.
Quindi
Per evitare di digitare ogni volta il comando Limit e il rimanente codice, definiamo una funzione che accetta come argomento la funzione di cui vogliamo calcolare il limite, il punto di accumulazione e la direzione di avvicinamento a tale punto:
Ad esempio, vogliamo calcolare il limite per x->2 della funzione:
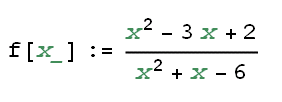
Abbiamo
Cioè il limite è 1/5
Tracciando il grafico della funzione in un intorno di x0 di ampiezza sufficientemente piccola, troviamo:
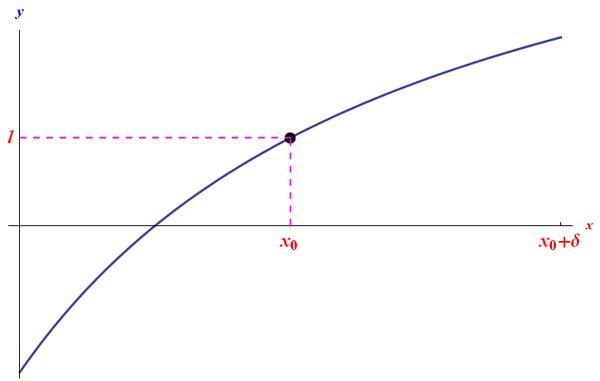
Per maggiori dettagli, scarica il file PDF contenente il codice Mathematica.
Indice delle Lezioni
Pacman
Nostradamus
Magical Cat Adventure
Snake