Lo zero nelle operazioni nell’insieme dei numeri naturali

Il numero zero è arrivato in Occidente grazie al popolo degli Arabi, i quali lo hanno appreso dagli Indiani. Fu il matematico Leonardo Pisano, detto Fibonacci, a far conoscere lo zero in Europa tramite il suo libro dal titolo “Liber abaci” (1202).

Fibonacci tradusse il termine “sifr”, usato dagli arabi per indicare lo zero, nel termine latino “zephirum”, da cui fu ricavato il termine veneziano “zevero” e, quindi, quello italiano “zero”.

Lo zero nell’addizione

Lo zero è quel numero che, sommato a qualsiasi numero naturale, lo lascia inalterato:

n+0=0+n=n

Per tale ragione viene detto “elemento neutro della somma“.

Lo zero nella sottrazione

E’ uguale a zero la somma tra due numeri naturali se il minuendo e il sottraendo sono uguali tra loro, cioè:

n-n=0

Lo zero lascia inalterato un numero naturale se si trova nella posizione di sottraendo, ovvero:

n-0=0

Invece, se esso si trova al posto del minuendo, si ha:

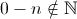
Per tale ragione non è elemento neutro per la sottrazione.

Lo zero nella moltiplicazione

Per questa operazione, lo zero ha il ruolo di elemento assorbente o elemento annullatore. Infatti:

Vale quindi, la seguente:

Legge di annullamento del prodotto. Il prodotto di due o più numeri è uguale a zero se e solo se almeno uno dei fattori è zero.

Lo zero nella divisione

Anche nel caso della divisione, è importante il posto occupato dallo zero perché origina comportamenti diversi.
Lo zero come dividendo rende nullo il quoziente, ovvero:

0:n=0

Lo zero come divisore, cioè:

n:0

fa sì che l’operazione non dia nessun risultato.

Lo zero sia come dividendo che come divisore, cioè:

0:0

rende indeterminato il risultato dell’operazione.

Lo zero nella potenza

Quando lo zero occupa il posto della base, allora fa sì che il risultato della potenza sia uguale a 0, cioè:

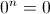
per ogni numero naturale n diverso da zero.

Se lo zero occupa sia il posto della base che quello dell’esponente, allora l’operazione non dà un risultato preciso, cioè:

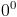
è una potenza indeterminata.

Se la base è un numero diverso da zero e l’esponente è uguale a zero, allora si avrà sempre: