Visto che ho poco tempo per scrivere vi propongo questo spassoso articolo del geniale sito/blog “In coma è meglio“, buona lettura.
Un fenomeno che non è stato ancora studiato con la dovuta attenzione è l’aggrovigliamento dei cavi. Si tratta di un fenomeno ben noto, in particolare a chi per professione o per diletto conduce una vita a stretto contatto con cavi, fili o cordicelle di vario genere, e può essere descritto come segue: presi due o più cavi in quiete e posti a piccola distanza fra loro, cioè a una distanza molto minore della loro lunghezza, essi si aggroviglieranno saldamente l’uno intorno all’altro come annodati da esperte mani di marinaio in un tempo molto inferiore a quello necessario per sbrogliarli e, soprattutto, senza l’intervento di nessun marinaio.
Se per esempio prendiamo due cavi A e B e li adagiamo su una superficie piana come in figura
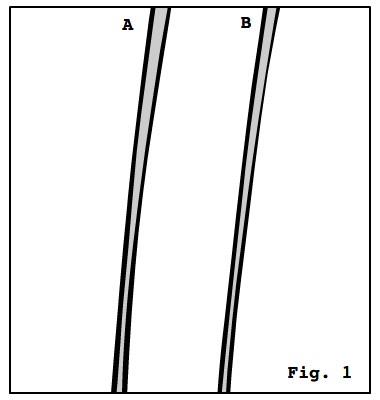
essi assumeranno rapidamente una delle seguenti configurazioni:
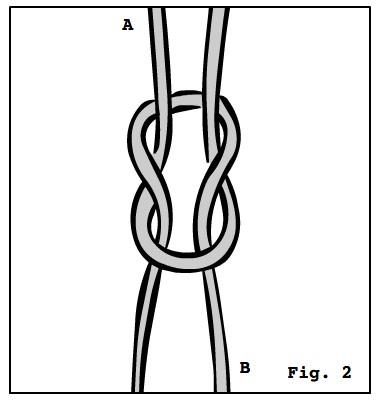
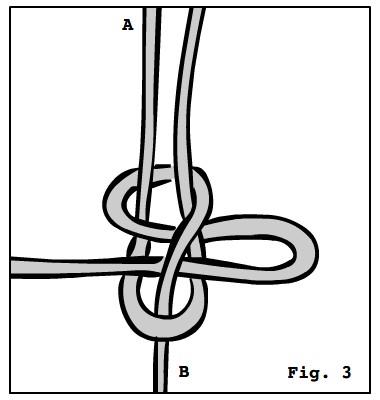
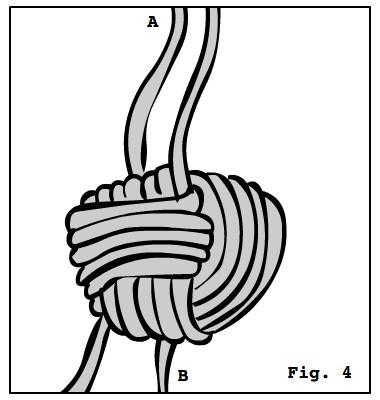
Qual è la causa di questo fenomeno? Pare che esista una forza di attrazione che si esercita fra le cose lunghe e sottili. Questa forza è detta “forza gordiana” e va ad aggiungersi alle altre forze fondamentali già note: gravitazionale, elettromagnetica, forte, debole e così così. Questa forza ha un raggio d’azione che è proporzionale alla lunghezza dei cavi, ma la sua intensità non dipende dalla distanza fra essi, bensì dalla loro utilità. Più i cavi sono utili, più si aggrovigliano. Se per esempio mettiamo due cavi di cui non ci frega assolutamente niente sul pavimento dello sgabuzzino e chiudiamo la porta per una settimana o due, quando torneremo a controllare li troveremo esattamente nella stessa posizione in cui li avevamo lasciati. Nei casi come questo la forza gordiana è nulla. Ciò è stato ampiamente verificato dal seguente esperimento condotto negli anni Novanta nei laboratori del Gran Sasso: si sono presi un centinaio di lacci da scarpe, li si è disposti a casaccio in una scatola di cartone e si è abbandonato il tutto in un sottoscala. La scatola non è stata ancora aperta, ma osservazioni in banda X confermano che i lacci sono ancora tutti come li si era lasciati, cosa che ha suscitato non poco scalpore nel mondo scientifico, tanto da far passare in secondo piano il fatto che i lacci da scarpe emettano raggi X.
Se invece uno si corica sul divano ad ascoltare la musica con gli auricolari collegati al computer, magari dando a vedere di sentirsi perfettamente comodo, il cavo dell’alimentazione e quello degli auricolari formeranno immediatamente un’unica grande matassa informe, impedendo qualunque tipo di movimento e avvolgendosi più e più volte intorno a tutto ciò che ha la forma di un collo umano.
Si può dunque concludere che la forza gordiana (F) è proporzionale all’utilità dei cavi (µ) e alla fretta di chi li usa (ƒ).
Dove a, b e c sono le prime tre lettere dell’alfabeto.
Se i cavi sono indispensabili e la fretta è smodata, la forza gordiana sarà così grande che nessuna bestemmia potrà controbilanciarla. In questo caso si avrà un collasso gordiano e la formazione dell’omonimo nodo. Questo spiega perché quando ci si allaccia le scarpe per andare in stazione a prendere il treno, i lacci formano un nodo di tale densità da far ripiegare su se stesse le dimensioni dello spazio-tempo. È la famosa teoria delle stringhe.
In futuro, quando si conoscerà un po’ meglio il meccanismo alla base dell’aggrovigliamento dei cavi, questa forza potrà forse essere sfruttata per produrre energia elettrica in apposite centrali a cavi. Basterà prendere degli uomini scalzi che devono perdere il treno, un treno e in mezzo un mucchio di scarpe.
Samuele su B-log(0), 2014. |
Permalink |
Nessun commento |
Aggiungi a
del.icio.us






