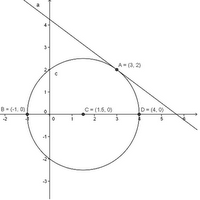
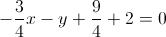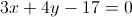Notiamo subito che in questo problema abbiamo già tre condizioni per poter determinare l'equazione della circonferenza. Essa infatti passa per il punto A(3;2) e dovendo passare anche per i punti di ascissa -1 e 4 dell'asse x, possiamo denominarli come B(-1;0) e D(4;0). Se imponiamo il passaggio della generica circonferenza per questi 3 punti, possiamo ottenere 3 equazioni in 3 incognite, che corrispondono proprio ai coefficienti a, b e c della generica equazione:
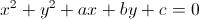Imponiamo il passaggio per B(-1;0):
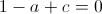Imponiamo il passaggio per D(4;0):
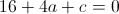E infine con A(3;2):
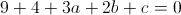Mettiamo a sistema le 3 equazioni per ottenere i valori di a, b e c:
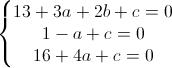Risolviamolo (salto qualche passaggio):
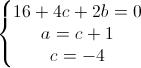
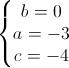Quindi l'equazione sarà:
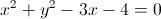Adesso determiniamo l'equazione della retta tangente alla circonferenza nel punto A(3;2). Innanzitutto, tale retta dovrà appartenere al fascio proprio di rette di centro A(3;2), per cui l'equazione di tale fascio in forma implicita sarà (per questa parte del problema vedi anche questo post):
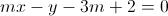Siccome la tangente è perpendicolare al raggio nel punto di contatto, allora possiamo ottenere il valore di m imponendo la condizione secondo cui la distanza della tangente dal centro della circonferenza sia uguale al raggio. Determiniamo pertanto le coordinate del centro C e la lunghezza del raggio r della circonferenza: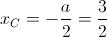
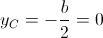Il centro ha coordinate C(3/2;0). Determiniamo la lunghezza del raggio:
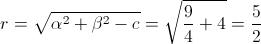Imponiamo ora che la distanza del centro C dalla tangente sia uguale al raggio, con la formula della distanza di un punto da una retta:
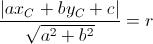Sostituiamo i valori e risolviamo rispetto a m: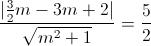 
Eleviamo ambo i membri al quadrato:
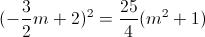
Otteniamo:
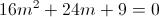
Risolviamo l'equazione di secondo grado rispetto a m ed otteniamo due radici reali e coincidenti:
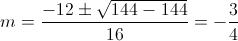
E l'equazione della retta quindi sarà, in forma implicita:
Pacman
Nostradamus
Magical Cat Adventure
Snake