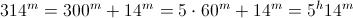Risolviamo il seguente problema:
Una cisterna di forma cilindrica ha il raggio di base di 20 dm ed è piena d'acqua. In quanto tempo viene vuotata da una pompa che estrae 120 litri d'acqua al minuto, sapendo che l'area della superficie laterale della cisterna misura 3768 dm^2?Per sapere in quanto tempo viene vuotata la cisterna,
è indispensabile innanzitutto determinare il volume dell'acqua all'interno di essa; infatti, se la pompa estrae 120 litri d'acqua in un minuto,
per capire quanto tempo essa impiega a vuotare la cisterna bisognerà capire qual è il volume d'acqua inizialmente presente. Per trovare il volume di un cilindro, la formula è:
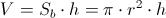
in cui l'area della superficie di base
Sb non è altro che l'area del cerchio di base, di cui conosciamo il raggio
r, mentre
h è l'altezza del cilindro-cisterna, di cui non conosciamo la lunghezza. Intanto possiamo calcolare l'area di base:
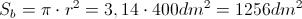
E' sicuramente più problematico ottenere l'altezza del cilindro, ma non è difficile. Se infatti è vero che:
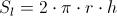
in cui
Sl rappresenta l'area della superficie laterale del cilindro,
varrà anche la formula inversa:
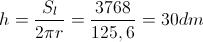
Il volume d'acqua contenuto quindi sarà:
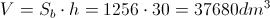
Ora, se la pompa estrae 120 litri d'acqua al minuto, quanto tempo sarà richiesto per estrarre 37680 litri (ricordiamo la corrispondenza tra litro e decimetro cubo)? Sarà sufficiente impostare una semplice proporzione:
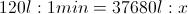
Da cui otteniamo
il tempo x:
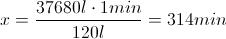E 314 minuti non sono altro che 5 ore e 14 minuti. Infatti:
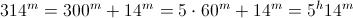
Una cisterna di forma cilindrica ha il raggio di base di 20 dm ed è piena d'acqua. In quanto tempo viene vuotata da una pompa che estrae 120 litri d'acqua al minuto, sapendo che l'area della superficie laterale della cisterna misura 3768 dm^2?Per sapere in quanto tempo viene vuotata la cisterna, è indispensabile innanzitutto determinare il volume dell'acqua all'interno di essa; infatti, se la pompa estrae 120 litri d'acqua in un minuto, per capire quanto tempo essa impiega a vuotare la cisterna bisognerà capire qual è il volume d'acqua inizialmente presente. Per trovare il volume di un cilindro, la formula è:
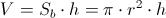in cui l'area della superficie di base Sb non è altro che l'area del cerchio di base, di cui conosciamo il raggio r, mentre h è l'altezza del cilindro-cisterna, di cui non conosciamo la lunghezza. Intanto possiamo calcolare l'area di base: 
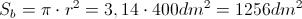E' sicuramente più problematico ottenere l'altezza del cilindro, ma non è difficile. Se infatti è vero che:
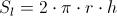in cui Sl rappresenta l'area della superficie laterale del cilindro, varrà anche la formula inversa:
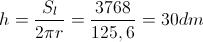Il volume d'acqua contenuto quindi sarà:
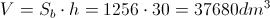Ora, se la pompa estrae 120 litri d'acqua al minuto, quanto tempo sarà richiesto per estrarre 37680 litri (ricordiamo la corrispondenza tra litro e decimetro cubo)? Sarà sufficiente impostare una semplice proporzione:
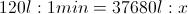Da cui otteniamo il tempo x:
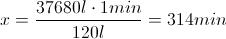E 314 minuti non sono altro che 5 ore e 14 minuti. Infatti:
Pacman
Nostradamus
Magical Cat Adventure
Snake