Per ciò che riguarda l'interpretazione geometrica della derivata, ci rimane da esaminare il caso dei cosiddetti punti cuspidali o semplicemente, cuspidi.
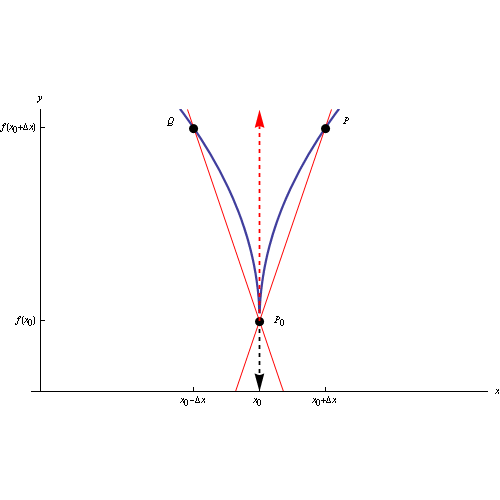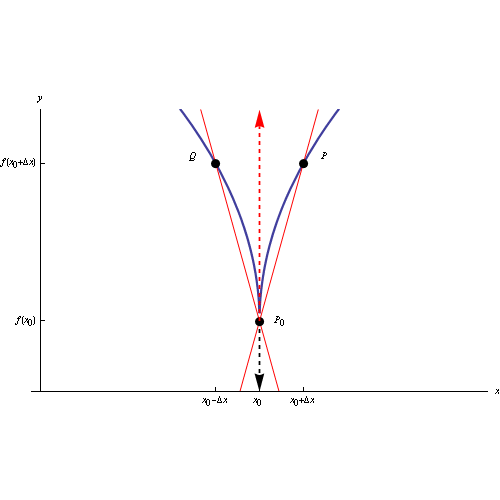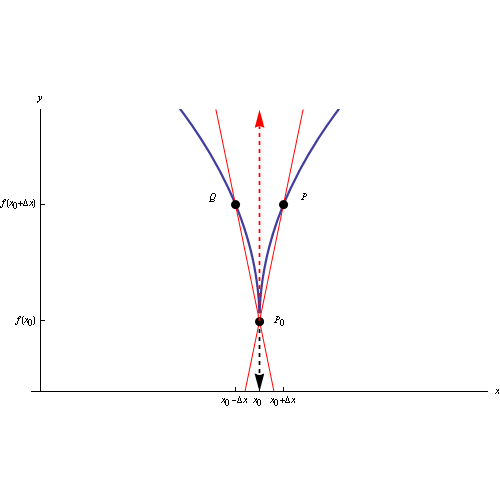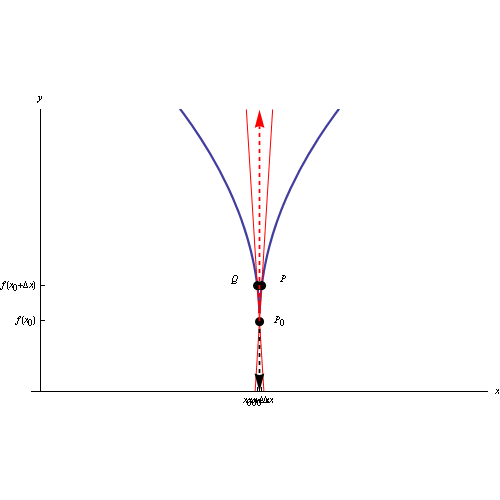
Il grafico di una funzione (continua in un assegnato intervallo) ha un punto cuspidale in P0(x0,y0) quando la funzione non è derivabile in x0, ma è dotata a sinistra e a destra di derivata infinita e di segno opposto. Senza perdita di generalità:
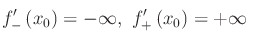
In tal caso la retta secante ha il seguente comportamento:
dove
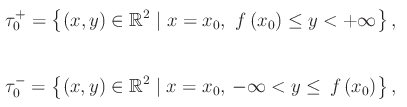
Tali luoghi geometrici si chiamano rispettivamente semitangente a destra e semitangente a sinistra, mentre il punto P0(x0,y0) si chiama punto cuspidale.
L'immagine al top del post è un'animazione in ambiente Mathematica che visualizza la posizione limite delle due secanti destra e sinistra, al tendere a zero dell'incremento della variabile indipendente. Al link seguente il codice Mathematica:
Puntocuspidale.pdf
Pacman
Nostradamus
Magical Cat Adventure
Snake