Punti di discontinuità della reciproca della funzione parte intera di x

Già conosciamo la funzione parte intera di x. Oggi studiamo i punti di discontinuità della sua reciproca: f(x)=1/[x].

La definizione di parte intera di un numero reale porge:

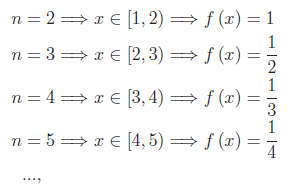
Ne consegue che il grafico della funzione assegnata è l'unione di infiniti segmenti semiaperti a destra, come illustrato nella figura al top di quest'articolo. Inoltre, ogni punto di ascissa intera è di discontinuità di prima specie. Il salto di discontinuità è s(n)=-1/(n-1).

Scarica l'handbook