Qual è l'ordine di infinitesimo di

Rammentiamo i concetti principali sugli infinitesimi.

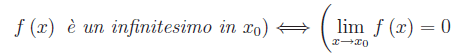
Se f(x) e g(x) sono due infinitesimi in x0, e se il rapporto f/g è ivi regolare, può accadere:

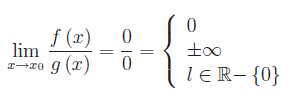
Nel primo caso diremo che f(x) è un infinitesimo di ordine superiore rispetto a g(x). Nel secondo, f(x) è un infinitesimo di ordine inferiore rispetto a g(x). Infine, nel terzo caso diremo che f e g sono infinitesmi dello stesso ordine.

Se il rapporto f(x)/g(x) non è regolare, si studia il comportamento di |f(x)|/!g(x)| e se nemmeno questo è regolare, vediamo se verifica la seguente proprietà:

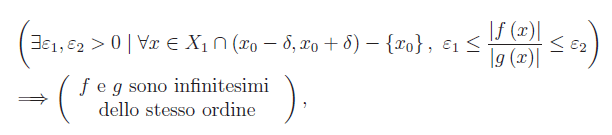
Cioè andiamo a vedere se il rapporto f/g è definitivamente limitato intorno a x0. Se non si verifica nemmeno questa circostanza, gli infinitesimi si dicono non confrontabili. Per rispondere al quesito che ci siamo posti, vale a dire il calcolo dell'ordine di infinitesimo (rispetto a g(x)=x) della funzione f(x)=x*sin(1/x), consultare il seguente file pdf.