Quante diagonali ha un poligono?

In qualsiasi poligono, si definisce diagonale un qualsiasi segmento di esso che abbia per estremi 2 suoi vertici non consecutivi. Non importa se il poligono sia concavo o convesso, perché una diagonale non necessariamente dev'essere contenuta interamente nel poligono, ma può anche essere esterna oppure attraversare parzialmente il poligono, come succede per alcune diagonali di poligoni concavi. Viene da sé che il poligono con il minimo numero di lati, ossia il triangolo, non può avere diagonali. E' inoltre errato credere che le sue diagonali coincidano con i lati, perché in un triangolo non è mai possibile avere una coppia di vertici non consecutivi, per cui crolla anche il senso stesso di un'eventuale diagonale.
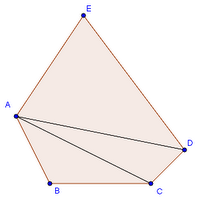
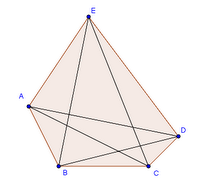
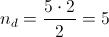Se consideriamo un quadrilatero, invece, è intuitivo disegnarvi 2 diagonali. Se però un poligono ha più di 4 lati, ad esempio se pensiamo di disegnare un poligono con 90 lati, siamo allo stesso modo pronti a rispondere? E' senz'altro più difficile, per cui conviene trovare un criterio e, di conseguenza, una formula matematica più generale che ci consenta di prevedere più facilmente il numero cercato. Procediamo con ordine, considerando a titolo di esempio un pentagono.
Se vogliamo contare le diagonali uscenti da un dato vertice, ad esempio A, non ci resta altro che considerare il numero di vertici non consecutivi con il vertice dato. Essi sono soltanto C e D, per cui da A usciranno 2 diagonali. Ci si rende conto quindi che il numero di diagonali uscenti da un vertice è n - 3, ossia pari al numero n di lati/vertici diminuito di 3, perché in sostanza, affinché si possa raggiungere l'altro estremo di una diagonale, a partire da un vertice, bisogna escludere il vertice stesso di partenza e i 2 vertici ad esso consecutivi. Quindi, il numero delle diagonali uscenti da un vertice è:

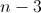
Se si estende lo stesso discorso all'intero poligono, ossia a tutti i vertici, allora dovremmo avere che il numero delle diagonali è:

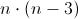
Bisogna tuttavia tenere presente che, se non dimezzassimo il numero così ottenuto, conteremmo anche dei "doppioni". A titolo di esempio, moltiplicando n * (n-3) conteremmo 2 volte tutte le diagonali, ma AD e DA sono la stessa diagonale, AC e CA idem, e così via. La formula generale per calcolare il numero di diagonali nd in un poligono è pertanto:

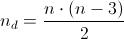
Applichiamo la formula al pentagono che abbiamo preso in considerazione prima, in cui n = 5.