I modelli di reti neurali artificiali (ANN) che hanno suscitato maggior interesse nelle applicazioni pratiche sono addestrati tramite la presentazione di casi nei quali gli output della rete desiderati sono noti. Talvolta, però, le ANN possono essere usate per scoprire patterns nei dati senza essere in possesso di nessuna altra informazione.
Questo tipo di reti neurali sono in genere composte da due soli strati di neuroni e l’addestramento può avvenire senza alcuna supervisione. La più famosa architettura di questo tipo consiste nella mappa di Kohonen. Teuvo Kohonen (1934) è un ricercatore, ed è attualmente professore emerito nell’accademia Finlandese. Uno dei suoi più famosi contributi fu quello sulle reti auto-organizzanti “SOM”. Il metodo di addestramento adottato da questo modello è denominato “competitive learning“, per via del fatto che nello strato di uscita avviene una vera e propria competizione.
Le reti SOM (Self-organizing maps) sono un particolare tipo di ANN che creano una forte ed interessante analogia con le reti biologiche che compongono la corteccia celebrale.
Questa corteccia può essere paragonata al cappello di un fungo che avvolge il suo gambo, i nuclei sottocorticali e il midollo spinale. Alla corteccia affluiscono le informazioni visive, acustiche, olfattive e le sensazioni tattili e dolorose: ogni sensazione è mappata e viene letta da una specifica area della corteccia. (area di differenza sensoriale).
Insieme a quest’area sensoriale, vi si trovano le aree motorie, che controllano la funzione dei muscoli volontari. E’ stato possibile tracciare una mappa dei neuroni responsabili dei movimenti delle dita, della mano, delle braccia e di tutti gli altri muscoli volontari. Siccome non tutte le aree muscolari sono uguali, c’è una differenza di sensibilità fra le diverse parti del corpo. La mappa dei movimenti, come quella delle sensazioni viene definita con il termine di “omuncolo” che indica la rappresentazione proporzionale delle funzioni motorie e sensoriali.
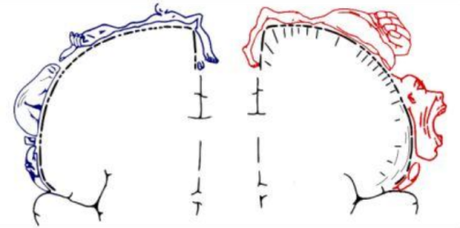
Figura 1: Omuncolo sensoriale e motorio
Le aree motorie si occupano di generare impulsi atti a contrarre le rispettive parti del corpo formate da muscoli volontari, mentre le aree sensoriali raccolgono informazioni dai vari organi recettori, più un’area sensoriale è ampia più la sensazione è ricca di dettagli.
Nelle reti SOM, i neuroni proiettano l’input multidimensionale su una superfice di neuroni artificiali, rappresentandolo in due dimensioni ed effettuandone quindi una notevole compressione, pur conservando le similarità originarie. Inoltre la capacità di scoprire, in modo autonomo, proprietà interessanti di un input multidimensionale accomuna le reti SOM alla capacità degli organismi viventi di adattarsi all’ambiente senza la necessità di una guida esterna. Le reti SOM sono in grado imparare in modo autonomo come classificare una serie di input attraverso la competizione fra i suoi neuroni che ne compongono la superficie.
Passiamo ora all’implementazione base delle reti SOM a livello matematico/informatico.
La seguente figura mostra i due strati, input ed output e la tipologia delle loro connessioni:
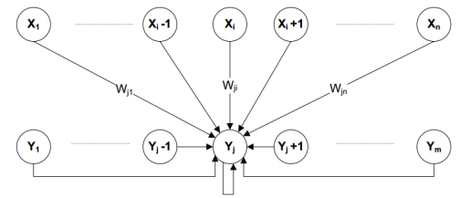
Figura 2: Interconnessioni rete SOM
Come descrive la figura, ‘n’ neuroni di input sono completamente collegati a ‘m’ neuroni di output tramite pesi ‘w’. Queste unità, sono ulteriormente connesse fra loro incluse loro stesse tramite pesi ‘v’. Lo strato di uscita è chiamato ‘mappa’. La mappa di Kohonen.
In questa mappa, i neuroni vicini si eccitano tra loro, mentre quelli lontani hanno funzione inibitoria. Questi insiemi di unità corrispondono al “vicinato“, questo per ogni neurone, esso costituisce la simulazione della connettività fisica costituita dalle sinapsi che collegano tra loro i neuroni di uscita. La descrizione matematica di quest’area corrisponde ad una funzione a “cappello messicano”. Dal punto di vista della programmazione questa è un’operazione molto utile, dato che utilizzare delle sinapsi reali di diverso valore per ogni neurone di uscita verso tutti gli altri sarebbe molto onerosa in termini sia di costo computazionale che di memoria necessaria. Teniamo presente che reti di questo tipo hanno generalmente centinaia o migliaia neuroni di uscita.
Figura 3: Distribuzione dei pesi del tipo “a cappello messicano” in un intorno del neurone Yj
Formalizzando, la dinamica della rete, ragionando sullo strato di uscita, dati j = numero di neuroni di uscita, k = estensione vicinato, i = numero di neuroni in entrata, corrisponde a:
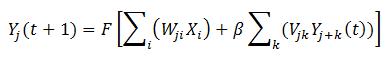
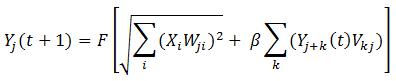
La dinamica della rete è molto semplice. Lo è ancora di più il metodo di aggiornamento dei pesi, che rispetto alle metodologie descritte in uno degli articoli precedenti riguardanti le reti feed-forward, cerca semplicemente di avvicinare il vettore dei pesi al vettore di input. (Si veda in [1] ).
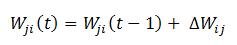
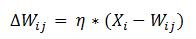
Riassumendo l’addestramento e il funzionamento della rete, abbiamo le seguenti fasi:
- Si inizializza la rete con M x N pesi sinaptici Wji (solitamente corrisponde ad una matrice)
- Si presenta in input il generico vettore X = {X1, X2, X3, … Xn) e si calcola l’attivazione dei neuroni di uscita secondo le equazioni viste in precedenza. Si trova così il neurone Yj con massima attivazione. (Spesso chiamato neurone vincente)
- Questo neurone viene premiato assieme a tutto il suo vicinato, aggiornandone i valori sinaptici. (Solo i pesi del neurone vincente e del suo vicinato vengono aggiornati.) Il coefficiente di addestramento viene fatto diminuire nel tempo con legge lineare, compresa anche l’estensione del vicinato che tende alla fine ad essere uguale all’unità.
- Questo procedimento viene eseguito per tutti i pattern X del training set. (ripeti da 2)
- Una volta che tutto il pattern set è stato somministrato l’operazione viene ripetuta completamente. Questo fino a che la classificazione è soddisfacente.
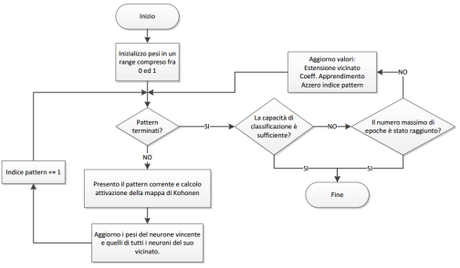
Figura 4: Flow-chart algoritmo di addestramento non supervisionato rete Self-organizing map
Molto spesso si ricorre alle som semplicemente per “trasformare” dati multidimensionali in due dimensioni. (riga – colonna della mappa di Kohonen di uscita.) I dati, ridotti in due dimensioni, vengono in genere trattati ulteriormente da altri classificatori.
Come si stabilisce se una rete som è addestrata se il tipo di addestramento non è supervisionato?
E’ chiaro che nel caso dell’addestramento supervisionato il processo termina quando la corrispondenza input – output desiderata viene raggiunta. In questo caso non avendo alcun errore da valutare al termine di ogni epoca di addestramento, è una buona pratica controllare il massimo aggiornamento avvenuto nell’ultima epoca. Quando questo sarà uguale a 0, significa che la convergenza è stata raggiunta.
Una delle operazioni fondamentali da eseguire quando si lavora con reti SOM, è la normalizzazione degli input.
E’ molto importante per assicurare la convergenza dell’addestramento che i dati di ogni pattern vengano normalizzati in input e che siano congrui ai valori con cui abbiamo inizializzato i pesi. Per esempio, se i nostri pattern sono costituiti da vettori di valori compresi fra 1 e -1, essi risultano correttamente mappati con i pesi anche essi compresi in questo range. Se invece gli input sono compresi in un range 0 e 1, mentre pesi iniziati fra -1 e 1. l’addestramento ne soffrirà. Questo tema è bene affrontato in [2].
Il metodo più diffuso, è la normalizzazione Z-Axis.
Questo metodo modifica e aggiunge un extra input s per ogni pattern.
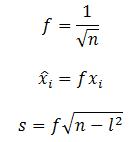

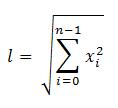
Assumiamo per esempio che queste serie rappresentino dei profili altimetrici.
Abbiamo quindi un set di addestramento:
// Training set
double set[20][input_u] = {
0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1,
1,0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1,0,
0.2,0.3,0.5,0.4,0.6,0.7,1,0.9,0.8,0.1,0,
0.5,0.4,0.3,0.2,0.1,0,0.1,0.2,0.3,0.4,0.5,
0,0.25,0.5,0.75,1,1.25,1.5,1.75,2,2.25,2.5,
2,1.88,1.76,1.64,1.52,1.4,1.28,1.16,1.04,0.92,0.8,
1,2,3,4,5,6,7,8,9,10,11,
12,11,10,8,7,6,5,4,3,2,1,
1,2,0.5,0.8,1.1,1.5,1.8,1.9,1.5,1.3,1,
0.34,0.45,0.67,0.7,0.87,1,1.2,1.5,1.78,1.9,2,
2,1,1,2,3,4.5,5.66,7.8,9,1.1,1.3,
0.2,0.4,0.3,0.45,0.5,0.47,0.6,0.66,0.8,0.81,0.9,
0.54,0.85,0.97,1.15,1.37,1.47,1.8,2.16,2.58,2.71,2.9,
0.68,1.125,2.233333333,3.5,8.7,1.428571429,12,7.5,5.933333333,4.75,4,
0.68,1.225,2.433333333,3.8,9.1,1.928571429,12.6,8.2,6.733333333,5.65,5,
1.68,2.125,3.233333333,4.5,9.7,2.428571429,13,8.5,6.933333333,5.75,5,
1.88,2.425,3.733333333,4.9,10.3,3.128571429,14,9.4,7.733333333,5.85,5,
3,2,1,0,1,2,3,4,5,6,7,
2.8,1.7,0.5,-0.4,0.4,1.3,2,3.1,4.2,5.9,7,
1,1,1,1,1,1,1,1,1,1,1
};
E uno di valutazione:
// Validation set
double vset[6][input_u] = {
0.2,0.4,0.6,0.8,1,1.2,1.4,1.6,1.8,2,2.2,
0.15,0.25,0.35,0.45,0.55,0.65,0.75,0.85,0.95,1.05,1.15,
1,0.76,0.52,0.28,0.04,-0.2,-0.44,-0.68,-0.92,-1.16,-1.4,
2,2,2,2,2,2,2,2,2,2,2,
1,1,1,1,1,1,1,1,1,1,1,
1.88,2.425,3.733333333,4.9,10.3,3.128571429,14,9.4,7.733333333,5.85,5
};
Utilizzando una rete som con 11 input (ogni pattern ha 11 valori di altitudine) e una mappa di Kohonen costituita da 16 x 16, ovvero 256 unità di uscita, presentando il set di addestramento per alcune decine di epoche di presentazione, ho ottenuto sul set di valutazione queste classificazioni: (i valori di uscita sono stati normalizzati tramite metodo zero-max)
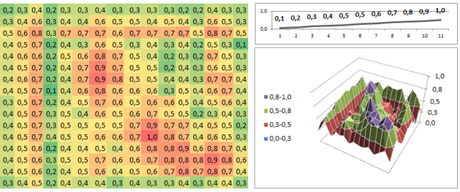
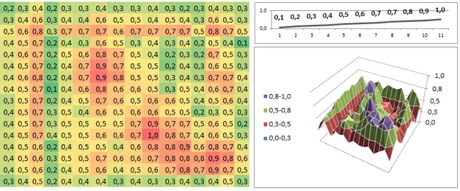

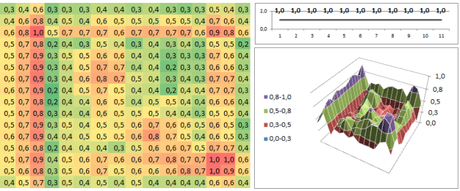
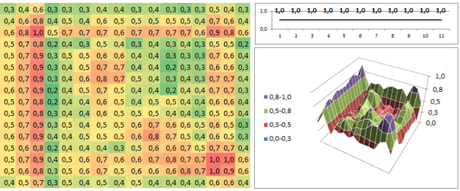
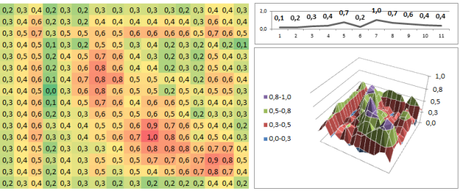
Come è evidente, emerge spontaneamente una classificazione delle caratteristiche dei dati.
Nel primo pattern di valutazione la pendenza positiva (salita) risulta essere mappata nell’area in basso a destra dove si raggiunge il massimo valore di attivazione, caratteristica presente anche nell’ultimo pattern, in effetti calcolando la tendenza totale dell’ultima serie, risulta essere una serie con pendenza positiva, per questo probabilmente la classificazione risulta essere molto simile.
La pendenza negativa (discesa) sembra essere mappata nell’area sinistra in basso, mentre il piano in alto a sinistra.
Risultati migliori si ottengono con una più efficiente mappatura dei dati (infatti i valori negativi erano molto pochi mentre i pesi sono inizializzati fra -1 e 1) e più valori per la descrizione del profilo altimetrico, oppure, senza dubbio, tramite un algoritmo di addestramento per som che sia invece supervisionato. Articoli di ricerca avanzati sulle SOM sono [3],[4] e [5].
Bibliografia:
.1 Silvio Cammarata – Reti neuronali. Dal perceptron alle reti caotiche e neuro-fuzzy, ETASLIBRI, 1990
.2 Timothy Masters - Practical Neural Network Recipes in c++, ACADEMIC PRESS, 1993
.3 Jun-fei Qiao, Hong-gui Han, An adaptive fuzzy neural network based on self-organizing map, Beijing University of Technology China
.4 Jirı Dvorsky, Vaclav Snasel, Jana Kocıbova- Improvements Quality of Kohonen Maps Using Dimension Reduction Methods, Technical University of Ostrava Czech Republic
.5 Tobias Schreck – Visual-Interactive Analysis With Self-Organizing Maps – Advances and Research Challenges, Technische Universitaet Darmstadt, Computer Science Department, Interactive Graphics Systems Group Germany







