Trovare le dimensioni di un rettangolo sapendo il loro rapporto e l’area

Un tipico problema di geometria ci chiede di trovare le dimensioni di un rettangolo di cui conosciamo l’area ed il rapporto tra base ed altezza. Vediamo come risolverlo.

Problema: Un rettangolo ha l’area di 225 cm² e l’altezza è i quattro noni della base.

Per comprendere il procedimento è meglio disegnare la figura.

Se l’altezza è i 4/9 della base, questa sarà  9/9, quindi tutto il rettangolo è formato da 9×4=36 quadratini.

L’area di ciascun quadratino misura: area rettangolo diviso numero quadratini:

225 : 36 = 6,25 cm²

Adesso possiamo calcolare la lunghezza del lato di questo quadratino con la formula inversa che dice: lato quadrato = radice quadrata (area quadrato)

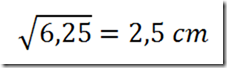
Infine calcoliamo la misura della base AB = 9 x 2,5 = 22,5 cm
e la misura dell’altezza BC = 4 x 2,5 = 10 cm