Proponiamo un semplice esempio in modo da capire i concetti fondamentali, che ci darà tra l'altro, la possibilità di calcolare la trasformata di Fourier a mano, cioè senza eseguire calcoli mostruosi. Supponiamo di avere una grandezza y variabile in funzione del tempo t, secondo la legge:
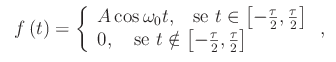
il cui grafico è:
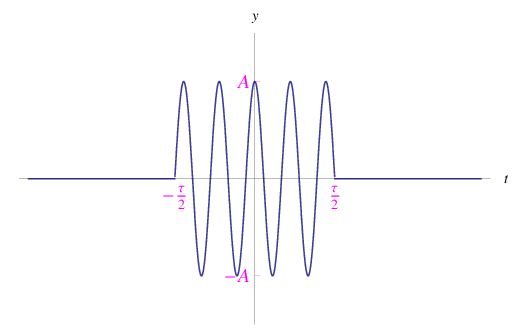
La grandezza f(t) non è periodica, ma è tuttavia esprimibile attraverso uno sviluppo in integrale di Fourier:
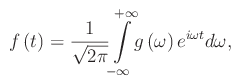
da cui vediamo che f(t) si esprime come una sovrapposizione lineare di infiniti termini monocromatici (o armonici o componenti di Fourier) di frequenza w variabile da -oo a +oo. La funzione g(w) è continua in (-oo,+oo) ed è tale che g(w)dw è l'ampiezza delle componenti di Fourier la cui frequenza è compresa tra w e w+dw. Ne consegue che la funzione g(w) è la densità spettrale nota anche come trasformata di Fourier della f(t).
Invertendo la relazione precedente:
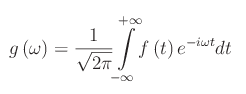
Per determinare la densità spettrale della funzione assegnata utilizziamo la notazione complessa:
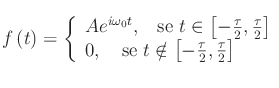
Calcolando l'integrale
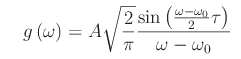
Vediamo che tale funzione è un'oscillazione sinusoidale modulata da (w-w0)^-1, come illustrato in figura:
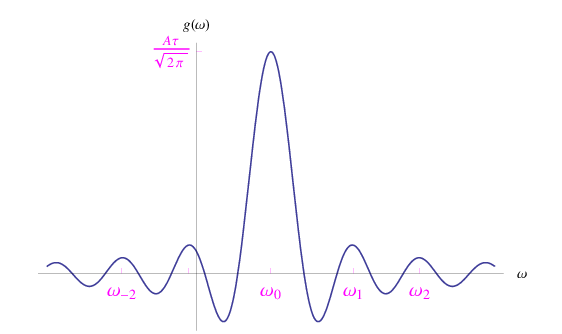
Il contributo dominante a f(t) proviene dalle componenti di Fourier con frequenza prossima a w0. D'altra parte, al crescere della durata del segnale, la densità spettrale diviene progressivamente più piccata intorno a w0, come mostrato dal grafico:
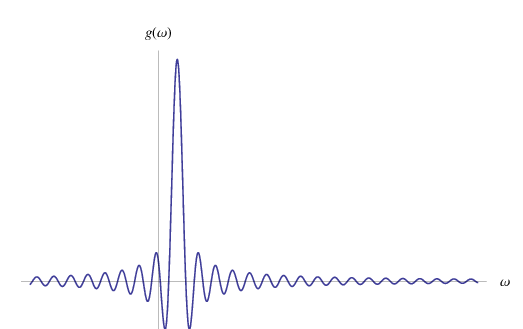
Al limite:
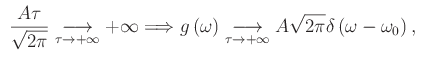
ritroviamo, in tal modo, la funzione delta di Dirac.
Inoltre:
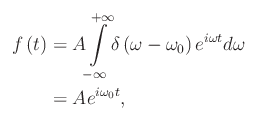
cioè la funzione assegnata (in notazione complessa) per t variabile ad -oo a +oo.
Viceversa, al diminuire di tau la distribuzione g(w) delle frequenze tende ad allargarsi, come mostrato dal grafico.
Scarica l'articolo in PDF: fourier000.pdf
Pacman
Nostradamus
Magical Cat Adventure
Snake