Qui andremo a soffermarci maggiormente sulle loro proprietà e su dettagli un po' più tecnici.
Ricordiamo innanzitutto che un numero complesso è nient'altro che una coppia ordinata (x, y) di 2 numeri reali x e y, generalmente rappresentati mediante la forma z = x + iy.
In particolare, i è l'unità immaginaria, x viene detta parte reale del numero complesso, mentre y ne designa la parte immaginaria.
In simboli:
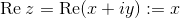
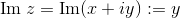
Nell'insieme dei numeri complessi ℂ vengono definite per ogni z₁ = x₁ + iy₁ e z₂ = x₂ + iy₂ le seguenti operazioni:
- addizione:
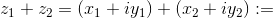
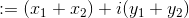
Nello stesso modo avviene la sottrazione (unica differenza è il segno):
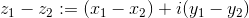
- moltiplicazione:
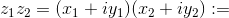
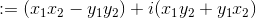
Come noto, i numeri complessi vengono rappresentati su un piano, chiamato piano complesso o piano di Argand-Gauss, costituito da un asse orizzontale passante per l'origine (il quale designa l'asse reale) e da un asse verticale passante per l'origine (detto asse immaginario).

L'unità immaginaria i = 0 + 1i verifica la relazione:
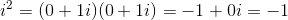
Ciò implica che, a differenza di quanto accade nel campo dei numeri reali, un'equazione come z² +1 = 0 ammette soluzione in ℂ.
Ricordiamo che il complesso coniugato di un numero complesso z è semplicemente il numero che viene ottenuto cambiando il segno della parte immaginaria di z.
In simboli:

Valgono le seguenti proprietà relative ai complessi coniugati:
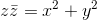
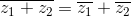
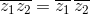
Per quanto concerne la divisione di 2 numeri complessi, si procede così: per dividere z₁ = x₁ + iy₁ per z₂ = x₂ + iy₂ si moltiplicano il dividendo e il divisore per un numero complesso che sia coniugato del divisore, ovvero x₂ - iy₂.
In simboli:
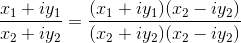
Per ogni numero complesso z definiamo modulo di z il numero reale non negativo |z|, che equivale a:
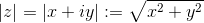
Il significato geometrico del modulo è ben spiegato dall'immagine seguente:

L'angolo compreso tra l'asse x e il vettore r, che denoteremo con φ, è denominato argomento di z o, in breve, arg z.

Ricordando le definizioni di seno e coseno relativamente ai triangoli rettangoli, si può constatare che:
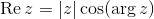
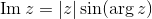
Compattando il tutto:
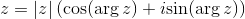
L'argomento di z non risulta definito se z = 0 e inoltre, se z ≠ 0, arg z è determinato a meno di un multiplo intero di 2π.
Dunque possiamo riscrivere il tutto come:
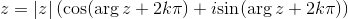
per ogni k intero se z ≠ 0.
Quella appena riportata è la rappresentazione trigonometrica dei numeri complessi, se z ≠ 0.
In generale, dato un numero complesso, non si riesce a determinare esplicitamente l'argomento, tuttavia sfruttando le formule sopra riportate è sempre possibile risalire al valore del seno e del coseno dell'argomento.
Elenchiamo ulteriori proprietà:
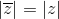
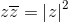

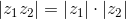
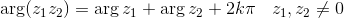
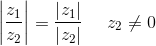
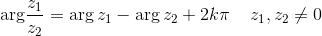
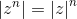
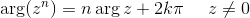
Se poi |z| = 1, cioè z = cos φ + i sin φ, allora si ricava la celebre formula di De Moivre:

Ancor più di carattere generale è la celebre formula di Eulero:
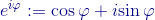
Grazie alla quale è possibile riscrivere la formula di De Moivre come:
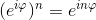
Osserviamo che:
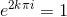
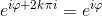
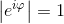
Da tali osservazioni, per ogni z ≠ 0, possiamo arrivare alla cosiddetta rappresentazione esponenziale dei numeri complessi:
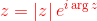
o analogamente:
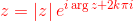
Dalla formula di Eulero si ricava anche che:
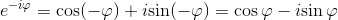
Ora con qualche trucchetto magico (cioè con qualche passaggio matematico) ricaveremo le espressioni del seno e del coseno dell'argomento in notazione esponenziale.
Procediamo!
Dall'ultima espressione isoliamo i sin φ:
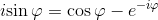
e sostituiamo quanto trovato nella formula di Eulero originale:
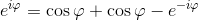
Da cui è facile ricavare che l'espressione del coseno sia eguale a:
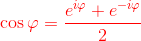
Ora è sufficiente sostituire quest'ultima uguaglianza in
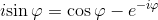
per ottenere facilmente:
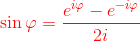
La notazione esponenziale dei numeri complessi è molto spesso utilizzata nelle applicazioni, giacché essa facilita abbondantemente le manipolazioni che coinvolgono le grandezze trigonometriche.
Non a caso, anche la nota serie di Fourier ha una sua forma esponenziale, basata sui numeri complessi!
Si consiglia al lettore non esperto la rilettura dell'articolo "Fourier e la sua serie", prima di avventurarsi nella trattazione che segue.
La formula di Eulero generalizzata

suggerisce appunto che una serie di Fourier si possa esprimere in forma più compatta utilizzando gli esponenziali complessi, al posto delle funzioni trigonometriche.
In particolare, per giungere a una formulazione differente della serie di Fourier si sfruttano le seguenti formule di Eulero (che abbiamo ricavato prima):

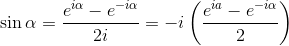
Per quest'ultimo passaggio si è adoperata la definizione di reciproco di un numero complesso.
Sia f(t) una funzione periodica di periodo T, sostituiamo ora i valori ricavati nella formula della serie di Fourier

ed effettuiamo le necessarie trasformazioni:




Poniamo ora:
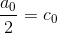
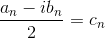
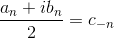
L'espressione diviene allora:
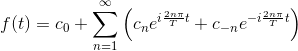
Risulta possibile esprimerla in forma maggiormente concisa:
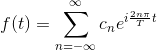
Questa è appunto la forma esponenziale della serie di Fourier, dove i coefficienti cn sono dati da:

È interessante notare che se la funzione f(t) è a valori reali, allora
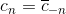
Per concludere, al fine di riposarci un po' dopo questo mare di formule, leggiamoci un bel passo di Storia dei simboli matematici di Joseph Mazur dedicato all'unità immaginaria i:
"Da quei primi inizi, quando le più antiche forme di conteggio ci attribuivano 10 dita, 2 occhi e un naso, il concetto di numero ha fatto passi da gigante. I numeri oggi non fanno più esclusivo riferimento alle sole cose che vediamo o che abbiamo bisogno di contare. La matematica moderna è interessata alle definizioni, ai ragionamenti e ai modelli che possono essere tradotti in forma simbolica. Purché le regole matematiche e la grammatica simbolica vengano rispettate, una definizione può anche contraddire il senso comumente attribuito alle parole o i concetti che ci sono intuitivi, in particolar modo i concetti fisici intuitivi. Esse aprono le porte a interi universi logici trascendenti la natura visibile. In nessun ambito questo aspetto appare tanto evidente quanto nell'estensione dei campi numerici al di là dei numeri razionali. Solo un linguaggio matematico puro, con un'impronta simbolica fortemente definita, può permettere di vedere al di là e capire cosa vi si possa trovare. Un tempo, l'idea che ci potesse essere un numero il cui quadrato avesse un valore negativo sembrava al di là di ogni immaginazione. Quale avrebbe potuto essere l'utilità di un oggetto immaginario come √-1? Se applichiamo correttamente la grammatica simbolica alla risoluzione dell'equazione x² - 2x - 2 = 0, troviamo 2 soluzioni ragionevoli 1+ √3 e 1-√3. Ma cosa salta fuori se tentiamo di applicare la medesima grammatica simbolica all'equazione quadratica x² - 2x +2 = 0? Uscirebbero 2 soluzioni strane: 1+√-1 e 1-√-1. Prendiamo una qualsiasi di queste soluzioni, eleviamola al quadrato, sottraiamole due volte se stessa e aggiungiamo 2. Cosa otteniamo? Zero. Separatamente, queste 2 soluzioni possono sembrare inutili, ma se le sommiamo otteniamo semplicemente 2. In altre parole, lo strano termine √-1 si elide nel processo di sostituzione all'interno dell'equazione. Se un lettore proveniente dal XVI secolo prendesse in mano questo capitolo, penserebbe - e farebbe bene a pensare - che c'è già qualcosa di sospetto nel sommare due numeri come 1+√-1 e 1-√-1 per ricavarne 2. Tale somma implica che √-1 - √-1 = 0. È vero? Una risposta moderna sarebbe: «Certo, x - x deve essere sempre uguale a zero, qualunque cosa sia x.» Certamente, tale relazione vale per i numeri che obbediscono alle normali regole dell'aritmetica. Ma finora, tutto quello che sappiamo è che √-1 è un simbolo che rappresenta qualcosa emerso come risultato di una manipolazione algebrica simbolica eseguita su un'equazione di 2° grado. Non sappiamo nulla su cosa sia √-1, a parte il fatto che rappresenta qualcosa di misterioso con una proprietà definitoria in base alla quale, «se lo moltiplichiamo per se stesso», qualunque cosa questo possa significare, «si ottiene il numero negativo -1». Il nostro lettore venuto dal passato potrebbe pensare che 1+√-1 e 1-√-1 siano soluzione prive di senso perché non vi è alcuna prova evidente che esistano fenomeni reali che conducono a un'equazione di secondo grado come x² - 2x +2 = 0 (in notazione attuale). Se il nostro lettore provenisse dalla fine del XVI secolo e sapesse qualcosa sulla rappresentazione grafica di equazioni di 2° grado in un sistema di coordinate rettangolare, potrebbe dirci che il grafico dell'equazione è una parabola il cui punto di minimo si trova in (0; 2), punto che si colloca 2 unità al di sopra dell'asse x, e che quindi non esiste alcun valore di x per cui il valore di y risulti 0. Ma proviamo a guardare oltre. Abbandoniamo le coordinate rettangolari e prendiamo in considerazione qualcosa di diverso. Cosa accadrebbe se ora ammettessimo nel nostro sistema di numerazione tutti i numeri della forma a+b√-1, dove a e b sono due numeri già ammessi nel club dei numeri reali? Si potrebbe pensare che sia sciocco includere numeri di questo tipo. Tuttavia, simbolicamente, qualunque cosa siano questi nuovi oggetti, essi si comportano in modo perfettamente coerente con la grammatica e la sintassi dei nostri numeri ordinari. Sembrano obbedire a tutte le leggi a cui obbediscono i numeri ordinari: se ne sommiamo due, ne sottraiamo due, ne moltiplichiamo due o ne dividiamo due, otteniamo sempre un altro oggetto della forma a+b√-1. Se si applicano tutte le usuali leggi di combinazione di numeri ai nuovi oggetti, esce sempre un risultato della stessa forma! Ma perché è così difficile - a differenza di quanto accade con i numeri normali come 1, 2, 3...ma anche con numeri meno conosciuti forse, come 3/4, π, o √2 - averne un'immagine chiara, capire in modo inequivocabile cosa possa rappresentare un numero come √-1 al di là dell'immagine simbolica a cui stiamo iniziando ad abituarci? Si potrebbe pensare che √-1 sia già un simbolo, e che esso rappresenti semplicemente la radice quadrata di -1 ma a ben guardare non è stato costruito a questo scopo. È emerso come conseguenza di manipolazioni algebriche nel tentativo di risolvere un'equazione . È come se, un po' per caso, il numero negativo -1 si fosse trovato imprigionato sotto un segno di radice quadrata nel corso del processo risolutivo. Osserviamo che, con un gioco di prestigio aritmetico, ogni numero della forma a+√-c, con a e c numeri reali, può essere scritto come a+b√-1, con a e b numeri reali. Quindi √-1 assume un ruolo e un'importanza particolari per cui risulta giustificato introdurre un simbolo speciale per indicarla. La indichiamo con la lettera i, iniziale della parola «immaginario». Forme rappresentate come bi, dove b rappresenta un numero reale, sono chiamate «numeri immaginari», e forme rappresentate come a + bi sono chiamate «numeri complessi», complessi per il fatto di essere una sorta di miscela di reale e immaginario. (Purtroppo, entrambe le parole - «immaginario» e «complesso» - si sono ormai stabilmente insediate nel vocabolario matematico. Purtroppo, perché le classi di numeri a cui si riferiscono non hanno nulla né di immaginario né di complesso). Può sorprendere far notare come il simbolo i (anche se si tratta di una semplice abbreviazione della parola «immaginario») presenti notevoli vantaggi rispetto alla scrittura √-1. Diciamo che, in matematica, tra il leggere a+b√-1 e il leggere a + bi c'è più o meno la stessa differenza che c'è tra mangiare una fragola con il naso tappato, senza poterne apprezzare quindi il sapore seducente, e il mangiare una fragola respirando normalmente. Perché numeri? Perché continuiamo a chiamare questi oggetti «numeri»? Un tempo concepivamo il numero come risultato dell'atto del contare oggetti: il numero era conteggio di qualcosa, fossero le dita di una mano, le dita dei piedi, pecore, giorni, dracme, occhi, orecchie o nasi. Poi siamo passati a un'idea di numero come misura di qualcosa, misura che potrebbe risultare frazionaria o addirittura irrazionale. Ma questi cosiddetti numeri complessi che cosa contano, cosa misurano? Forse sarebbe meglio chiamarli «coppie di numeri» ma anche così il nostro consueto senso di ciò che dovrebbe essere un numero non ne uscirebbe soddisfatto. E, in verità, non sono neppure coppie di numeri perché c'è sempre quella piccola cosa appiccicosa che si attacca al secondo numero della coppia.
Dei numeri interi abbiamo un'immagine mentale. Li concepiamo come disposti su una linea retta in modo che ogni numero intero venga posizionato a una distanza di un'unità dal numero precedente a partire dallo 0, i numeri interi positivi a destra, i numeri interi negativi a sinistra. Lo stesso potremmo dire per i numeri razionali e per i numeri reali, eventualmente prevedendo una loro rappresentazione a infinite cifre decimali...Per visualizzare i numeri complessi occorre qualcosa di molto più originale di una retta. Inizialmente, il concetto di numero era tradotto da un semplice aggettivo: «dieci» dita. Molto, molto più tardi divenne un sostantivo, «dieci», senza alcun riferimento a specifici oggetti unitari. Ma dalla metà del XVI secolo, quando i simboli iniziarono a diffondersi nel linguaggio della matematica, la definizione di numero cominciò gradualmente ad ampliarsi, a estendere i propri confini concettuali, arrivando a includere l'idea che il numero possa rappresentare un atto o una modalità di essere. Oggi, per noi il numero i è proprio questo, cioè un'azione: precisamente l'atto associato a una rotazione di 90 gradi...Quando la formula di Cardano per le soluzioni di equazioni polinomiali di 3° grado portò all'idea che i numeri immaginari - a dispetto del loro deplorevole nome - potessero risultare utili, anche i più autorevoli matematici e filosofi furono piuttosto sconcertati dai misteri collegati a tali nuovi numeri. Parte della colpa era da attribuirsi alla loro apparente inapplicabilità. Se a una rosa dessimo un altro nome, la rosa continuerebbe ad avere lo stesso profumo; se avessimo chiamato √-1 in qualunque altro modo che non fosse «numero immaginario», quel numero ci sarebbe apparso tanto reale quanto gli altri. Si tratta veramente di un nome infelice. I numeri negativi fecero la loro comparsa giocando con equazioni della forma x + a = b. Allo stesso modo, i numeri immaginari emersero giocando con equazioni della forma x² + a = b. Il significato di quest'ultima equazione dipende radicalmente dai valori assunti dai simboli a e b e dalla legittimità dell'operazione di estrazione di radice quadrata di numeri negativi. Finché a è minore di b, nessun problema. Quando invece a è maggiore di b, ci troveremmo di fronte a un numero che, moltiplicato per se stesso, è uguale a un numero negativo. Sarebbe un nonsenso, a meno che non decidiamo di ammettere nel club dei numeri anche le radici quadrate di numeri negativi. La qual cosa ci costringerebbe a riprendere in mano la questione fondamentale della matematica - che cos'è il numero? - per permetterci di dare un significato a tutte le soluzioni delle equazioni della forma x² + a = b. Vogliamo cioè che √(b-a) abbia significato sempre, per qualunque coppia di numeri razionali a e b. Forse, in qualche modo misterioso, è possibile dare piena legittimità al simbolo, apparentemente privo di senso, i, concependolo come qualcosa di molto più reale che immaginario. Forse quegli strani simboli, privi di senso, possono essere utilizzati in qualche modo per ricavare le soluzioni a determinati tipi di problemi matematici, ottenendone risultati pienamente validi. Whitehead, una volta, disse scherzando:
«Un simbolo che non sia stato ben definito non è neppure un simbolo. È solo una macchia di inchiostro su un foglio con una forma facilmente riconoscibile. Ma non si può dimostrare nulla con una successione di macchie, a eccezione dell'esistenza di una pessima penna e di uno scrittore disattento».
Un numero complesso x + iy si rivela essere nient'altro che una coppia di numeri reali (x; y) che obbedisce a una lista di regole semplici. Tale numero si dimostra incredibilmente utile nella risoluzione di problemi di fluidodinamica, problemi inerenti alla conduzione del calore, problemi di gravità o, ancora, di quasi tutti i problemi della fisica matematica...Uno dei tratti meravigliosi della matematica è che - grazie ai suoi migliori simboli - i suoi progressi ampliano il nostro sguardo sulle cose. Quando moltiplichiamo un numero reale per -1, trasformiamo un qualunque numero positivo in un numero negativo e un qualunque numero negativo in un un numero positivo. Dal punto di vista grafico, osservando la retta dei numeri reali, ciò significa aver prodotto una rotazione di 180° di tutta la semiretta di origine O, intorno al punto O stesso. Numeri che prima crescevano verso destra, adesso diventano numeri che crescono verso sinistra. Quando invece moltiplichiamo un qualsiasi numero complesso per i, quello che otteniamo è una rotazione del numero in senso antiorario di 90° nel piano bidimensionale. Non appena si cerca di costruire un sistema numerico tridimensionale basato sulla tripletta (x, y, z), si finisce inevitabilmente con lo scontrarsi con un problema legato a brutti oggetti chiamati «zero-divisori» (cioè numeri non nulli il cui prodotto è pari a 0), i quali incasinano non poco l'usuale algebra della risoluzione di equazioni. Così, si decide di saltare direttamente dallo spazio a 3 dimensioni a quello a 4 dimensioni, cioè alla successiva dimensione in cui è possibile dar vita a un sistema numerico che obbedisca alla proprietà associativa - cioè sia a ∙ (b ∙ c) = (a ∙ b) ∙ c - e che non presenti zero-divisori. Per tutto questo c'è un prezzo, ovviamente: siamo costretti ad abbandondare la proprietà commutativa. In tale sistema, cioè, a ∙ b non è più uguale a b ∙ a. I «quaternioni», come vennero definiti dal matematico irlandese del XIX secolo William Rowan Hamilton, appartengono a un nuovo sistema numerico in 4 dimensioni che contiene i numeri complessi e un sistema moltiplicativo che obbedisce a tutte le leggi dell'algebra, a eccezione della proprietà commutativa. Hamilton scoprì i quaternioni durante una passeggiata con la moglie a Dublino. «In quel momento sentii chiudersi il circuito galvanico del pensiero; e le scintille che ne sprizzarono furono le equazioni fondamentali che collegano i, j, k; esattamente nella forma in cui le avevo sempre usate da allora»."

