
Tra le innumerevoli notiziole che finiscono per sovraffollare le bacheche di Facebook e/o le mitologiche colonne destre dei siti web dei grandi quotidiani, una è stata portata alla mia attenzione negli scorsi giorni (articoli di Panorama e Wired, rilanciate anche da altri siti, come Radio105).
L’annuncio è ad effetto:
Homer Simpson aveva scoperto il bosone di Higgs ben 14 anni prima del CERN.
Lo dimostrerebbe qualche fotogramma tratto dalla puntata L’inventore di Springfield, in cui vediamo il nostro eroe intento a riempire una lavagna di formule, una delle quali permetterebbe di calcolare la massa della “particella maledetta” (e non “particella di Dio”, per carità!).
Ora, prima di tuffarci in amene disquisizioni sulla plausibilità dell’annuncio (a scanso di equivoci: non è vero!), credo sia sensato chiedersi se ne valga la pena: I Simpson sono una serie comica, non certo Superquark.
Non sarà che sono soltanto un bacchettone privo di senso dell’umorismo?
Ai posteri l’ardua sentenza.

C’è in effetti un senso in cui tale lavagnata di cose sbagliate, implausibili, o comunque non sostenute dalla maggioranza della comunità scientifica è autenticamente sottile e divertente (i dettagli più avanti).
Tuttavia, il gioco regge se l’attenzione del pubblico (che assumo essere un insieme molto eterogeneo di persone) non viene deliberatamente e superficialmente pilotata su alcuni dettagli (che autonomamente non sarebbe in grado di apprezzare).
Mi spiego: immagino che, quando la scena venne trasmessa nel 1998, pochi spettatori riconobbero i simboli sulla lavagna, ancora meno capirono lo scherzo.
La grande maggioranza si perse dunque la strizzata d’occhio degli autori ma visse felice: NESSUNO si sognò di affermare che Homer avesse appena scoperto il bosone di Higgs.
Del resto, provo a figurarmi invece la stessa scena accompagnata da un sottotitolo gigante: “Gentili telespettatori, vi invitiamo a notare come Homer abbia appena scoperto il bosone di Higgs e, già che c’era, confutato pure l’ultimo teorema di Fermat” (c’entra pure lui!).
Il tutto dato in pasto a non addetti ai lavori, senza alcun commento a margine.
Non avrebbe granché senso.
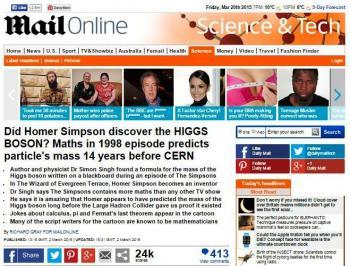
La riduzione italiana delle sue dichiarazioni suona appunto più o meno così:
"Homer Simpson aveva scoperto il bosone di Higgs ben 14 anni prima del CERN"
Il tutto, a mio avviso, rende un cattivo servizio sia agli autori della serie sia alla collettività.
Chiunque, infatti, legga l’articolo sarà portato in buona fede a credere a quanto riportato e a diffondere la notizia, allo stesso modo in cui potrebbe raccontare agli amici di quanto sia rimasto colpito dalla scoperta del gene XY in relazione alla cura della malattia Z, di cui ha appreso dal TG Leonardo.
Con la differenza che nel secondo caso la notizia sarebbe stata riportata in modo circostanziato, nel primo no.
Appurato che (anche) le notizie tecniche hanno bisogno di essere riferite in modo preciso e non fuorviante, cerchiamo di approfondire le ragioni per cui il buon Homer continua a non costituire un concorrente temibile per i ricercatori di tutto il mondo, e tuttavia il fotogramma “incriminato” sia degno di nota.

Per i meno avvezzi, ricordiamo che il bosone di Higgs è una particella elementare necessaria per formulare il Modello Standard [leggi qui il nostro articolo a riguardo], ad oggi la più completa teoria delle interazioni fondamentali di cui i fisici delle particelle possono disporre.
Il Modello Standard ha richiesto vari decenni di lavoro per essere perfezionato, è oggi alla base degli esperimenti in corso al Large Hadron Collider (LHC per gli amici) e ancora non si è ottenuto alcun risultato sperimentale che lo contraddica.
Anzi, molte tra le più accurate misure mai effettuate confermano in modo spettacolare le predizioni della teoria (cfr. momento magnetico dell’elettrone).
Il bosone di Higgs era l’unico mattoncino di questo edificio ancora sfuggito all’osservazione (mica per niente “particella maledetta”!), finché nel luglio 2012 il CERN ne ha annunciato la scoperta.
Cosa significa scoprire il bosone di Higgs?
Per quanto ne so, non può che voler dire verificarne l’esistenza, dal punto di vista sperimentale.
Ma allora non si scopre una particella elementare scrivendo su una lavagna! Serve un acceleratore, servono dei rivelatori (in breve, serve LHC), senza trascurare l’apporto fondamentale di migliaia di ricercatori che analizzano e interpretano l’enorme mole di dati registrata dalla macchina.
Che si intendesse - allora - l’aver intuìto la necessità dell’esistenza di una tale particella, e aver capito quanto essa è fondamentale per poter perfezionare il famoso modello di cui sopra che descrive il mondo alla scala subatomica?
In tal caso, è ben difficile che Homer sia arrivato per primo: gli articoli che "inventano" ciò che ora conosciamo come "meccanismo di Higgs" e postulano l’esistenza dell’omonimo bosone sono comparsi nel volume 13 di Physical Review Letters del 1964 (come ricordato anche durante le celebrazioni per i 50 anni della rivista).
Vale la pena ricordare che tre sono i gruppi di autori che, quasi in contemporanea, hanno avuto l’idea: Robert Brout e François Englert; Peter Higgs indipendentemente; Carl Hagen, Gerald Guralnik e Thomas Kibble. In tempi in cui la comunicazione delle scoperte avveniva unicamente per mezzo delle riviste cartacee, e passavano mesi dalla consegna di un articolo alla sua effettiva pubblicazione, è qualcosa di notevole.
Ridimensioniamo dunque la questione e chiediamoci se la formula dell’inventore di Springfield produca almeno il risultato corretto per la massa del bosone.
Compaiono varie costanti fondamentali:
- la costante di struttura fine α, che è legata alla carica elettrica dell’elettrone e dà una misura dell’intensità dell’interazione elettromagnetica;
- la costante di Planck h, fondamentale in meccanica quantistica;
- la velocità della luce c;
- la costante di gravitazione di Newton G, che compare nella formula per l’attrazione tra due corpi celesti che si studia a scuola.
La combinazione delle ultime tre — come scritto sulla lavagna — è (un multiplo di) un’altra costante, la massa di Planck.
La formula di Homer, alla resa dei conti, è dunque sensata dal punto di vista delle dimensioni fisiche delle grandezze coinvolte (cioè non si sta misurando una massa nelle unità, che so, di una velocità o di una forza! Non si sta dicendo "questo barattolo pesa sette metri al secondo"!).
Detto ciò, se ci si arma di calcolatrice e si sostituiscono i numeri ai simboli corrispondenti, si trova un valore per M(H0) che si discosta significativamente da quello misurato nella realtà: 774 GeV/c2 invece di 125 GeV/c2 (perdonate le strane unità di misura, si tratta comunque di energie divise per velocità al quadrato, cioè di masse).
Dal punto di vista di Singh, non va così male: si tratta di un valore “solo un po’ più grande di quello poi rivelatosi corretto”. Personalmente non sono d’accordo, la discrepanza mi sembra rilevante, anche perché vari argomenti teorici portavano a ritenere molto più plausibile l’idea di un bosone di Higgs “leggero”, vicino ai 125 GeV/c2 (valori più bassi della massa erano già stati esclusi da esperimenti precedenti).
Naturalmente è privo di senso fare eccessivamente le pulci: nel contesto scherzoso è tutto molto carino e persino credibile.
Non si venga a dire, però, che ciò significhi scoprire una particella!

La seconda uguaglianza che appare sulla lavagna è apparentemente un controesempio clamoroso a un celeberrimo risultato matematico, la cui storia è avvincente ed è raccontata ad esempio nel libro L’ultimo teorema di Fermat, scritto proprio da Simon Singh.
Il teorema afferma che, fissato un numero intero maggiore di 2, NON esistono altri tre numeri interi a,b,c che soddisfino l’equazione
an + bn = cn (una specie di generalizzazione del teorema di Pitagora, per cui le soluzioni esistono eccome, con n=2).
L’uguaglianza di Homer sembrerebbe smentire tale tesi (la cui dimostrazione fu pubblicata nel 1995 e valse la medaglia Fields ad Andrew Wiles), per n=12, a=3987, b=4365, c=4472.
Ora, la cosa buffa è che provando a verificare l’uguaglianza su una comune calcolatrice, se ne ha conferma! Ma l’arcano è presto svelato. Tali semplici calcolatrici possono mostrare solo poche cifre (tipicamente non più di dieci), ma qui si ha a che fare con numeri enormi, dell’ordine di 1043: per intenderci, 1 seguito da 43 zeri, da leggersi dieci milioni di miliardi di miliardi di miliardi di miliardi.
Con un computer si può verificare che, le prime 10 cifre di 398712 + 436512 e di 447212 sono identiche, cioè i due membri sono uguali a meno di una parte su dieci miliardi (ma tale differenza ammonta pur sempre a circa un milione di miliardi di miliardi di miliardi!).
Questo “quasi” accordo classifica la terna (3987, 4365, 4472) come una quasi-soluzione (near-miss solution) dell’equazione del teorema di Fermat.
David Cohen, uno degli autori de I Simpson, ha raccontato di aver congegnato di proposito lo scherzo, in modo che le ordinarie calcolatrici dessero conferma della (non) uguaglianza!

Qualche parola sulle ultime due righe della lavagna di Homer può essere trovata in un articolo di Singh per Slate, uscito nel 2013 (no, non sono ciambelle: hanno anche loro un senso).
Alternativamente, specie per chi volesse approfondire qualche tecnicismo, a questo link si trovano dei dettagli interessanti.
Andrea Orta
@twitTagli
P.S.: Nei link in testa all’articolo, non compaiono le maggiori testate giornalistiche, che paiono non aver rilanciato la notizia. Ciò fa loro onore.






