Ancora uno, poi di problemi non ne scrivo più. Almeno per un paio di giorni.
Il Calendario dell'Avvento 2014 si chiude con un problema proposto nel 1999 dalla Canadian Mathematical Society.
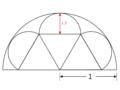
Nell'immagine è riportata una figura geometrica composta da tre semicerchi costruiti sui lati di tre triangoli equilateri uguali, e completata dal semicerchio esterno, su cui poggiano i triangoli equilateri, e che è tangente ai tre semicerchi.
Se il raggio del semicerchio esterno misura 1, quanto misura il raggio dei tre semicerchi interni?
Questo problema è un esempio di come la figura che lo accompagna possa facilitare oppure offuscare la strada verso la soluzione.
L'esempio classico al riguardo è il problema che avevo proposto molti post fa: sembra complicato, ma sarebbe risultato banalissimo se la figura avesse riportato l'altra diagonale del quadrato.
Nel nostro caso ho facilitato riportando il raggio del semicerchio interno, ma sarebbe stato ancora più semplice se il raggio del semicerchio esterno fosse stato disegnato in un'altra posizione.
Buona Vigilia.
[Tutti i post su numeri e giochi.]
Pacman
Nostradamus
Magical Cat Adventure
Snake