Elman neural networks

La previsione di ogni tipo di serie di dati o pattern, che variano nel tempo è l’impiego principale delle reti di Elman.
Una serie di dati può rappresentare l’andamento di vendite relativo ad un prodotto, la domanda di mercato, un pattern di comportamento sociale, la ripetizione di certi termini in una frase o altre sequenze simili.

Jeffrey Locke Elman, professore di scienze cognitive in California, Los Angeles. In [1] presenta una variante di rete neurale artificiale di tipo feed-forward dotata di memoria.

Questo tipo di reti differiscono dalle normali multilivello, per l’aggiunta di un ulteriore strato di neuroni per ogni layer nascosto. Questi neuroni conservano lo stato di attivazione del livello al quale sono collegati reintegrandolo alla successiva iterazione.

Per meglio capire la dinamica della rete possiamo assumere questo livello aggiuntivo, chiamato “context layer“, nel modo seguente:

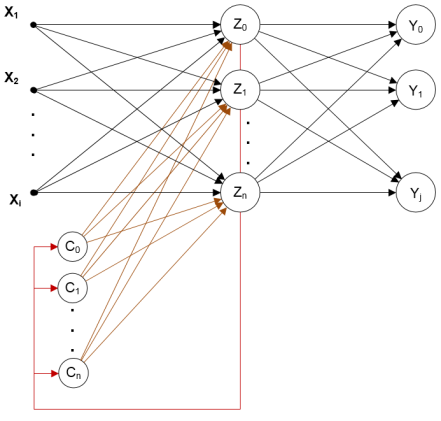
Figura 1: Struttura comune di una rete di Elman

Uno strato di ‘n‘ neuroni, dove ‘n‘ è pari al numero di neuroni nascosti, tiene in memoria il valore di uscita dello strato nascosto e lo ripropone come input.

Le connessioni che riportano l’output delle unità nascoste ai neuroni contesto hanno pesi di valore unitario e non sono soggette ad aggiornamenti (conn. rosse in fig. 1). Per le altre connessioni valgono le normali regole di addestramento, infatti è in questo modo che la rete ha possibilità di “apprendere” dagli errori commessi in passato (conn. arancioni in fig. 1). Si capisce come queste connessioni assieme allo strato di contesto costituiscono la memoria della rete.

L’equazione che determina il valore di uscita dei neuroni nascosti, rispetto ciò che conosciamo nelle normali reti multilivello, diventa:

Dove nella prima sommatoria, ‘i’ (-> ‘n’) è pari al numero di neuroni di input, nella seconda sommatoria, ‘n’ (-> ‘c’) è indice del neurone di contesto, ovviamente ogni strato di contesto ha numero di neuroni pari al rispettivo strato nascosto, quindi nell’equazione abbiamo anche che “c = j”.
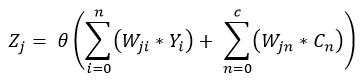
Inoltre, siccome abbiamo detto che il valore dei neuroni di contesto, non è nient’altro che il valore di uscita del rispettivo neurone all’iterazione precedente:

(Ricordando qui gli indici: “n = j”)
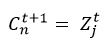
Possiamo riscrivere la formula come:

Per il problema della previsione, viene presentato alla rete un ‘training set’ costituito da pattern con ‘n‘ valori di input e altri ‘n‘ valori di output, questa coppia deve ovviamente rappresentare due parti contigue della serie di dati.
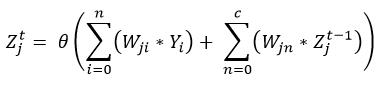
A scopo di esempio, se dovessimo insegnare alla rete come contare in base decimale, avremmo in input un pattern di dati tipo: 1,2,3,4,5 e 6,7,8,9,10 per la prima iterazione, poi aumentato di 1 alla seconda, quindi 2,3,4,5,6 e 7,8,9,10,11 e così via…
A fine addestramento la rete, in questo caso costituita da 5 input e 5 uscite, restituirà in uscita i cinque valori successivi i cinque forniti.

Per rendere più chiare le capacità di previsione della rete, il seguente esempio mostra una applicazione sviluppata a scopo dimostrativo che accetta in input qualsiasi sequenza mostrando in output i valori successivi predetti. Ammettiamo di voler insegnare alla rete la funzione ‘seno’: