Il Millenario Problema Dello Scivolamento Del Palo E Il Teorema Di Pitagora

Ragazzi di 2° B, ci stiamo addentrando sempre di più nello studio del Teorema di Pitagora e, non volendo accontentarci delle sole relazioni aritmetiche con cui si calcola un lato del triangolo rettangolo, noti gli altri due, abbiamo cercato di comprenderne il suo più profondo significato geometrico.
Da tale punto di vista, infatti, abbiamo compreso che il Teorema di Pitagora è un importantissimo problema di equiestensione (vedere il post dedicato). Abbiamo visto l'altro giorno come Bronowski ne spiega il significato in un video tratto dalla fortunata trasmissione della BBC degli anni settanta  "The Ascent of Man" (vedere il post Bronowski sul Teorema di Pitagora).Ma non ci basta ancora perché vogliamo saperne di più, vogliamo arrivare al millenario diagramma di argilla, che ci aspetta nel nostro laboratorio scolastico (leggere Lettera dello scriba).
Ma prima analizziamo il millenario problema dello scivolamento del palo o della canna, di cui ci parla il nostro caro amico Aldo Bonet nel suo splendido lavoro "Genesi del  teorema di Pitagora" (leggere il post specifico).
Riporto dal documento le parole con cui lo introduce Aldo:

Il “Teorema di Pitagora”, uno dei due tesori della geometria, come scrisse Keplero, è un argomento ancora dibattuto dagli storici riguardo alla sua origine e paternità.
Anche se ormai è chiaro che è una leggenda quella del teorema legato al nome di Pitagora in quanto era conosciuto, non come “teorema generale” ma in forma di “regola generale”, almeno 1000 anni prima di Lui, dalle civiltà mesopotamiche che lo applicavano per la soluzione di un diffusissimo problema, noto come  “ il problema dello scivolamento del palo o della canna” conosciuto peraltro in tutte le antiche civiltà potamiche: Sumeri, Indiani, Cinesi ed Egizi, (Ved. Storia dell’Algebra, S. Maracchia, Liguori, 2005/09, da pag.102 a pag.107); un problema che ho matematicamente dimostrato essere legato (o forse meglio generato) alla contemplazione del diagramma d’argilla a modulo quadrato, l’antico e primigenio strumento algebrico di risoluzione in uso comune presso le sopracitate antiche civiltà.
Forse, il motivo del legame di questo teorema al nome di Pitagora è dovuto al fatto che fu il primo a tentarne uno svincolo di sudditanza al millenario diagramma d’argilla, a cui era vincolato, per adattarlo al più pratico papiro (l’internet dell’antichità) col solo uso dei più “moderni” strumenti quali erano all’epoca: riga e compasso. Un “teorema” che Pitagora trovò ampiamente applicato nelle rinomate e millenarie scuole mesopotamiche durante i suoi viaggi, importandolo così nella Magna Grecia, e precisamente a Crotone; ecco ciò che probabilmente vide e importò Pitagora dall’antica Babilonia..."

Ebbene, è arrivato il momento di affrontare  l'arcaico problema dello scivolamento del palo o della canna, così intimamente connesso con il Teorema di Pitagora. Ve ne ho parlato proprio oggi e vi ho detto che il nostro Marco, altro grande amico, ci ha fatto la sorpresa di realizzare un applet interattiva con GeoGebra su questo problema. (Il link alla fine del post)
Leggete prima con attenzione l'intero problema preso da "Genesi del teorema di Pitagora" di Aldo.
 UN NOTO PROBLEMA DELLE CIVILTÀ ARCAICHE: TAV. B.M. 85196 N°9

Vi è indubbiamente una somiglianza incredibile tra la matematica babilonese, quella cinese, egizia e indiana (anche tra la stessa matematica babilonese seleucida (III sec a.C.) e quella più antica (II millennio a. C.) tanto che ha fatto avanzare ad alcuni storici, e in modo particolare, a B.L. van der Waerden, un’origine matematica comune, anteriore a quella babilonese più antica, la quale, aveva già una matematica sviluppata e che fa pertanto presupporre l’esistenza di una matematica addirittura ancora più antica o pre-babilonese, forse di origine sumerica; personalmente, anche le mie ricerche vanno decisamente in questa direzione, nella direzione di un'unica e forse più vasta Civiltà Madre delle origini.

Una delle notevoli somiglianze che vanno a sostegno di questa ipotesi è l’applicazione, nonché la risoluzione pressoché identica tra le civiltà potamiche sopra indicate,  di un primitivo e particolare problema, assai diffuso già nell’alta antichità e noto come: il problema dello scivolamento del palo o della canna.

Un problema che implica, per la sua soluzione, la conoscenza precisa del “Teorema di Pitagora” e, come vedremo, perfettamente applicato. Il problema n°9 che si trova ad esempio, nella tavoletta babilonese BM 85196, considerata tra le più antiche, propone di calcolare di quanto si discosta alla base di un muro, un palo di canna inizialmente accostato verticalmente o aderente ad esso e di lunghezza nota d, se questo scivola verso il basso di una certa misura n anch’essa assegnata. Dello stesso tipo è il 24° problema del papiro del Cairo (I sec a.C)

Testo n° 9 BM 85196: Un palo (o una canna) lunga 30 posto verticalmente contro un muro, è disceso di 6 verso il basso. Di quanto si è allontanato alla base del muro?

 TAVOLA G

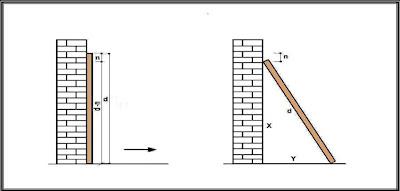
Dati del problema: n = 6; d = 30; Y =?
Questi sono i calcoli algebrici dello Scriba, tradotti da Thureau-Dangin, Textes Mathématiques Babyloniens, 1938, pag 42, 43, che traduco qui di seguito algebricamente:

Il testo si conclude con queste parole: “Questo è il modo di operare”.

Fin qui, l’antico Scriba babilonese (antenato di Pitagora) dimostra una perfetta applicazione e la sua conoscenza del “Teorema di Pitagora”, ma, poiché i teoremi a quell’epoca, come Pitagora di Samo, non esistevano ancora, questa applicazione era meglio conosciuta come una regola, quella che io ho coniato come: la regola generale babilonese, la quale a mio parere, fu scoperta e visualizzata, attraverso l’arte costruttrice o edile, col diagramma d’argilla a modulo quadrato come abbiamo esaurientemente visto nelle TAVOLE A e B precedenti e quelle allegate alla fine di questo articolo.
Lo Scriba, avrebbe preventivamente preso e quadruplicato un modellino in scala del palo, ottenendone quattro per farli coincidere imprimendoli nelle rispettive diagonali di quattro mattoni rettangolo d’argilla fresca, e mettendoli poi in gioco dentro il noto diagramma d’argilla risolvente.

Un diagramma che, secondo il mio pensiero, dagli ingombranti mattoni originari con cui si materializzò, fu sostituito poi nel tempo con laterizi di minor ingombro e spessore, fino a quando, con la maggiore diffusione del papiro e della carta, i Cinesi lo sostituirono con il più comodo cartoncino colorato che veniva ritagliato in figure geometriche movimentabili e sovrapponibili al diagramma, il quale, riecheggiava la memoria del più antico e tradizionale diagramma d’argilla progenitore, mantenendo così inalterati, sia il modello, sia la tecnica, sia un metodo di tassellatura a movimento rigido che determinò l’antichissima regola generale babilonese, fatta coi mattoni e che fu l’archetipo algebrico-geometrico quale patrimonio comune a tutte le arcaiche civiltà potamiche.
Leggere Karine Chemla, Matematica e cultura nella Cina antica, Matematica, i luoghi e i tempi, a cura di C. Bartocci e P. Odifreddi, Einaudi Editore, 2007, da pag.91 a pag. 137; vedere inoltre:
Teorema di Pitagora su Wikipedia
oppure su Progetto Polymath.

 E adesso l'immagine esportata dall'applet realizzata da Marco con GeoGebra.

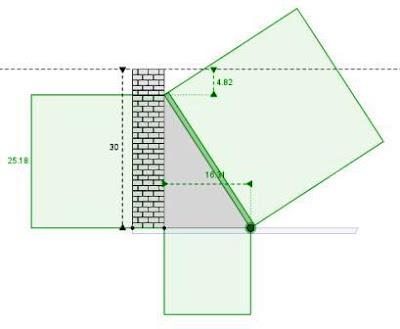
Avviate l'applet interattivo sul problema dello scivolamento del palo.