La costruzione dell'ennagono regolare

Colgo l'occasione per pubblicare un contributo gentilmente realizzato per questo blog da un fedele lettore, Paolo De Ponte, frutto di un proprio studio personale. Se avete dubbi, critiche costruttive oppure desiderate chiarimenti al riguardo, pubblicate un commento qui o sulla pagina facebook di Natura Matematica, vi risponderà Paolo. Grazie.
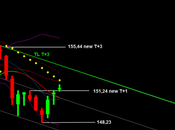
La costruzione dell'ennagono regolare risulta da sempre imposssibile per il semplice fatto che impossibile è anche la costruzione geometrica di un angolo con valore ɑ = 40°. E da sempre si è cercata una costruzione che desse un valore quanto più approssimato ad ɑ = 40°. Ad oggi, le scienze matematiche danno quale migliore risultato ottenuto con compasso 'senza memoria' e righello 'cieco' l'approssimazione per difetto pari ad  ɑ = 0,00094°, ottenuta con una costruzione tanto lunga e complessa che sul grafico dinamico del link che vado a pubblicare nel commento a seguire si rendono necessari due stop per fare 'pulizia' delle curve e delle rette precedentemente tracciate e ormai superflue.Desidero pubblicare su questa pagina la costruzione che ho realizzato e che, oltre a risultare molto più semplice, al punto da poterla presentare tramite uno schizzo artigianale, ha un'approssimazione per eccesso che è di oltre 12 volte migliore di quella, anch'essa per eccesso, della soluzione summenzionata, attualmente ritenuta la più vicina allo zero. Esattamente  ɑ = 0,00007479 ° contro ɑ = - 0,00094°

COSTRUZIONE CON RIGHELLO 'CIECO' E COMPASSO 'SENZA MEMORIA'
Premessa:Dati l'arco X-W di un angolo con ɑ = 60° e raggio 'r', si costruisce al suo centro l'arco A-B di un angolo ɑ = 15°. Conducendo dagli estemi della corda A-B le perpendicolari verso la base dell'angolo ɑ = 60°, ci deve necessariamente essere lungo il raggio 'r' un punto 'E'  tale che l'arco passante per esso trisechi  l'angolo  ɑ = 60° in modo chele altre due corde risultanti dalla trisezione ed esterne ad A-B siano uguali ad A-B.
Procedimento:1 - Come già detto, l'arco A-B è  pari ad ¼ dell'arco X-W, entrambi gliarchi divisi al centro da C-'O' ;2 - sia la lunghezza di 'O'-D pari a ¾ di 'r';3 - trovato il punto H al centro del raggio 'O'-C, si divida per 10l'emiraggio 'O'-H ( sezionabile con teorema di Talete o simile),quindi si faccia ruotare il segmento 'O'-S di 90° sino al punto N ;4 - con centro in D  e raggio D-N si tracci l'arco N-M, con M sulprolungamento dell'asse C- 'O' ;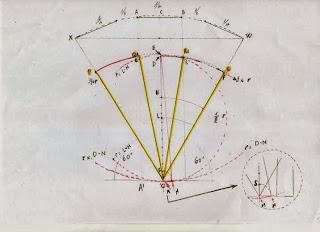5 - si indivui il centro L di  'O'-D e, con centro L e raggio L-M, siriporti il punto M lungo l'asse 'O-C'. Esso cadrà nel punto E, al disopra del punto D ;6 - con  centro 'O' e raggio 'O'-E si costruisca l'arco P-G passante per E;7 - la coppia d'archi P-Q + Q-R oppure R-G + Q-R costituirà  l'arco di un angolo con valore ɑ = 40,00007668° (s.e.& o.)
Misure:1 - Dato raggio r = 148, la corda  A-B sarà pari a 38,6357529;2 - H-'O' = 74.3 - S-'O' = 'O'-N = 7,44 - D-N = D-M = 'O'-E = 111,24639325 - Poiché sappiamo che l'arco centrale Q1-R1 ha una corda uguale a quella di A-B, ovvero 38,6357529, possiamo ricavare il valore dell'angolo Q1-'O'-R1  che risulterà essere ɑ = 20,00014958°.6 - Dall'operazione: (minuendo ɑ = 60°; sottraendo: ɑ = 20,00014958° ; risultato: 39,99985042)  e quindi dividendo il risultato per 2 otteniamo il valore degli angoli 'gemelli' P-'O'-Q1 e R1-'O'G, ovvero ɑ = 19,9999271°.7 - Per quanto sopra, l'angolo P-'O'-R o, a scelta, Q-'O'-G, ha un valore di ɑ = 40,00007479° (s.e.& o.)"Testo e costruzione geometrica in figura di Paolo De Ponte