
Un problema di geometria piana risolto per voi e per la nostra lettrice Stefania.
Problema: Disegna un cerchio di area 225 π cm2 e centro O. Da un punto E esterno alla circonferenza che dista dal centro i 5/3 del raggio conduci le tangenti EC ed EB alla circonferenza. Disegna il rettangolo ABCD inscritto nella circonferenza. Calcola perimetro ed area del pentagono ABECD.
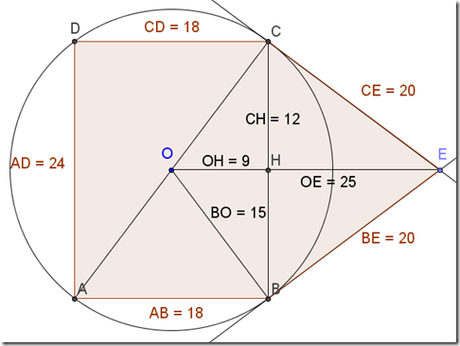
Soluzione:
Formula:
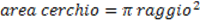
Formula inversa:
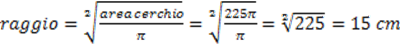
Raggio = AO = OC = 15 cm
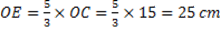
Le tangenti formano un angolo retto = 90° con il raggio, quindi il triangolo OCE è un triangolo rettangolo.
Con Pitagora trovo
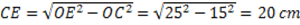
Trovo l’area del triangolo rettangolo OCE:
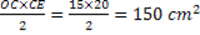
Con formula inversa, trovo l’altezza del triangolo rettangolo OCE:
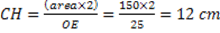
Quindi AD = BC = CH x 2 = 12 x 2 = 24 cm
Con Pitagora trovo HE
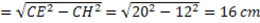
Con Pitagora trovo AB
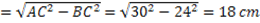
Perimetro del pentagono ABECD = 18 + 20 + 20 + 18 + 24 = 100 cm
Area del pentagono ABECD
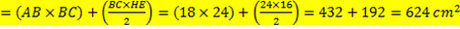
![[¯|¯] Algebra commutativa CoCoA](https://m22.paperblog.com/i/254/2541655/algebra-commutativa-con-cocoa-L-dO5nvg-175x130.png)

![[¯|¯] Coefficiente attrito dinamico tempo frenata](https://m22.paperblog.com/i/253/2535219/coefficiente-di-attrito-dinamico-e-tempo-di-f-L-FxxhyX-175x130.jpeg)
![[¯|¯] Epicicloidi Ipocicloidi](https://m22.paperblog.com/i/253/2531322/epicicloidi-ipocicloidi-L-7xp8az-175x130.jpeg)
