
Risolviamo il problema:
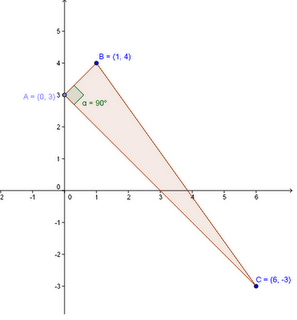
I vertici di un triangolo hanno coordinate A(0;3), B(1;4) e C(6;-3). Scrivere l'equazione dei suoi lati e dimostrare che esso è rettangolo.Risoluzione:Innanzitutto, individuiamo su un sistema di assi cartesiani ortogonali i vertici del triangolo in oggetto.
Per determinare l'equazione dei lati, basterà applicare la formula dell'equazione di una retta noti 2 punti di essa, per ciascuna delle rette individuate dai segmenti dei 3 lati. La formula è:
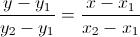
Applichiamola volta per volta a ciascuno dei 3 lati del triangolo.
 1) Per la retta su cui giace il lato AB:
1) Per la retta su cui giace il lato AB:
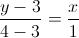
E l'equazione è:
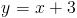 2) Per la retta su cui giace il lato BC:
2) Per la retta su cui giace il lato BC: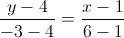
E l'equazione è:
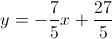 3) Per la retta su cui giace il lato AC:
3) Per la retta su cui giace il lato AC: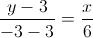
E l'equazione è:
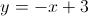
Ora ci resta da determinare se il triangolo sia o meno rettangolo. Potremmo seguire due strade: dal momento che abbiamo le 3 equazioni,
se riusciamo a trovare una coppia di lati tali che le loro equazioni abbiano coefficienti angolari l'uno antireciproco dell'altro, allora vuol dire che il triangolo ha un angolo retto e, pertanto, è rettangolo;
oppure determiniamo la lunghezza dei lati e verifichiamo la validità del teorema di Pitagora. Quest'ultimo è un procedimento più lungo perché prima dovremmo trovare la lunghezza dei 3 lati con la formula della distanza tra due punti e poi verificare la validità del teorema di
Pitagora. Seguiremo pertanto il primo.
Se osserviamo le equazioni delle rette dei lati AB e AC, notiamo che la prima ha coefficiente angolare uguale a 1, mentre il coefficiente angolare della seconda è -1, il suo antireciproco. Dunque le rette sono tra loro perpendicolari e il triangolo ABC è rettangolo in A.
 Risolviamo il problema:I vertici di un triangolo hanno coordinate A(0;3), B(1;4) e C(6;-3). Scrivere l'equazione dei suoi lati e dimostrare che esso è rettangolo.Risoluzione:Innanzitutto, individuiamo su un sistema di assi cartesiani ortogonali i vertici del triangolo in oggetto. Per determinare l'equazione dei lati, basterà applicare la formula dell'equazione di una retta noti 2 punti di essa, per ciascuna delle rette individuate dai segmenti dei 3 lati. La formula è:
Risolviamo il problema:I vertici di un triangolo hanno coordinate A(0;3), B(1;4) e C(6;-3). Scrivere l'equazione dei suoi lati e dimostrare che esso è rettangolo.Risoluzione:Innanzitutto, individuiamo su un sistema di assi cartesiani ortogonali i vertici del triangolo in oggetto. Per determinare l'equazione dei lati, basterà applicare la formula dell'equazione di una retta noti 2 punti di essa, per ciascuna delle rette individuate dai segmenti dei 3 lati. La formula è: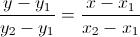 Applichiamola volta per volta a ciascuno dei 3 lati del triangolo.
Applichiamola volta per volta a ciascuno dei 3 lati del triangolo.  1) Per la retta su cui giace il lato AB:
1) Per la retta su cui giace il lato AB: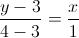 E l'equazione è:
E l'equazione è: 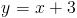 2) Per la retta su cui giace il lato BC:
2) Per la retta su cui giace il lato BC: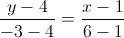 E l'equazione è:
E l'equazione è: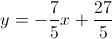 3) Per la retta su cui giace il lato AC:
3) Per la retta su cui giace il lato AC: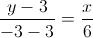 E l'equazione è:
E l'equazione è: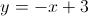 Ora ci resta da determinare se il triangolo sia o meno rettangolo. Potremmo seguire due strade: dal momento che abbiamo le 3 equazioni, se riusciamo a trovare una coppia di lati tali che le loro equazioni abbiano coefficienti angolari l'uno antireciproco dell'altro, allora vuol dire che il triangolo ha un angolo retto e, pertanto, è rettangolo; oppure determiniamo la lunghezza dei lati e verifichiamo la validità del teorema di Pitagora. Quest'ultimo è un procedimento più lungo perché prima dovremmo trovare la lunghezza dei 3 lati con la formula della distanza tra due punti e poi verificare la validità del teorema di Pitagora. Seguiremo pertanto il primo.Se osserviamo le equazioni delle rette dei lati AB e AC, notiamo che la prima ha coefficiente angolare uguale a 1, mentre il coefficiente angolare della seconda è -1, il suo antireciproco. Dunque le rette sono tra loro perpendicolari e il triangolo ABC è rettangolo in A.
Ora ci resta da determinare se il triangolo sia o meno rettangolo. Potremmo seguire due strade: dal momento che abbiamo le 3 equazioni, se riusciamo a trovare una coppia di lati tali che le loro equazioni abbiano coefficienti angolari l'uno antireciproco dell'altro, allora vuol dire che il triangolo ha un angolo retto e, pertanto, è rettangolo; oppure determiniamo la lunghezza dei lati e verifichiamo la validità del teorema di Pitagora. Quest'ultimo è un procedimento più lungo perché prima dovremmo trovare la lunghezza dei 3 lati con la formula della distanza tra due punti e poi verificare la validità del teorema di Pitagora. Seguiremo pertanto il primo.Se osserviamo le equazioni delle rette dei lati AB e AC, notiamo che la prima ha coefficiente angolare uguale a 1, mentre il coefficiente angolare della seconda è -1, il suo antireciproco. Dunque le rette sono tra loro perpendicolari e il triangolo ABC è rettangolo in A.







