Risolviamo il seguente problema:
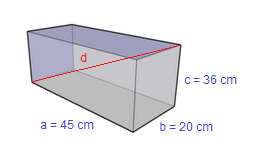 Una scatola a forma di parallelepipedo rettangolo ha le tre dimensioni lunghe 20 cm, 36 cm e 45 cm. Determina la lunghezza della diagonale e l'area della superficie totale della scatola.
Una scatola a forma di parallelepipedo rettangolo ha le tre dimensioni lunghe 20 cm, 36 cm e 45 cm. Determina la lunghezza della diagonale e l'area della superficie totale della scatola.La prima richiesta del problema è di determinare la lunghezza della diagonale del parallelepipedo. Per il calcolo della diagonale
d la formula è:
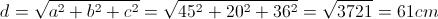 La spiegazione di questa formula deriva dall'applicazione del
La spiegazione di questa formula deriva dall'applicazione del teorema di Pitagora. Infatti nel triangolo rettangolo avente come ipotenusa
d e come cateto minore
c, indicando con
d' il cateto maggiore (che coincide con la diagonale del rettangolo di base) si avrà per il teorema di Pitagora:
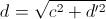
Ma applicando nuovamente il teorema di Pitagora al triangolo rettangolo avente come cateti
a e
be come ipotenusa
d' (in poche parole ciascuno dei due triangoli rettangoli in cui si può immaginare di dividere il rettangolo di base secondo una sua diagonale), avremo:
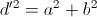
Da cui, con un'opportuna sostituzione:
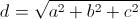 Per il calcolo dell'area della superficie totale
Per il calcolo dell'area della superficie totale (
St) del parallelepipedo
basterà sommare l'area della superficie di ciascuna coppia di facce opposte congruenti del solido, ossia:
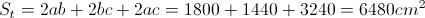
Se vuoi vedere un altro esempio di problema svolto su un prisma retto, vai a questo
link.
 Una scatola a forma di parallelepipedo rettangolo ha le tre dimensioni lunghe 20 cm, 36 cm e 45 cm. Determina la lunghezza della diagonale e l'area della superficie totale della scatola.La prima richiesta del problema è di determinare la lunghezza della diagonale del parallelepipedo. Per il calcolo della diagonale d la formula è:
Una scatola a forma di parallelepipedo rettangolo ha le tre dimensioni lunghe 20 cm, 36 cm e 45 cm. Determina la lunghezza della diagonale e l'area della superficie totale della scatola.La prima richiesta del problema è di determinare la lunghezza della diagonale del parallelepipedo. Per il calcolo della diagonale d la formula è: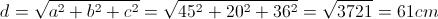 La spiegazione di questa formula deriva dall'applicazione del teorema di Pitagora. Infatti nel triangolo rettangolo avente come ipotenusa d e come cateto minore c, indicando con d' il cateto maggiore (che coincide con la diagonale del rettangolo di base) si avrà per il teorema di Pitagora:
La spiegazione di questa formula deriva dall'applicazione del teorema di Pitagora. Infatti nel triangolo rettangolo avente come ipotenusa d e come cateto minore c, indicando con d' il cateto maggiore (che coincide con la diagonale del rettangolo di base) si avrà per il teorema di Pitagora: 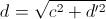 Ma applicando nuovamente il teorema di Pitagora al triangolo rettangolo avente come cateti a e be come ipotenusa d' (in poche parole ciascuno dei due triangoli rettangoli in cui si può immaginare di dividere il rettangolo di base secondo una sua diagonale), avremo:
Ma applicando nuovamente il teorema di Pitagora al triangolo rettangolo avente come cateti a e be come ipotenusa d' (in poche parole ciascuno dei due triangoli rettangoli in cui si può immaginare di dividere il rettangolo di base secondo una sua diagonale), avremo: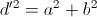 Da cui, con un'opportuna sostituzione:
Da cui, con un'opportuna sostituzione: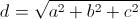 Per il calcolo dell'area della superficie totale (St) del parallelepipedo basterà sommare l'area della superficie di ciascuna coppia di facce opposte congruenti del solido, ossia:
Per il calcolo dell'area della superficie totale (St) del parallelepipedo basterà sommare l'area della superficie di ciascuna coppia di facce opposte congruenti del solido, ossia: 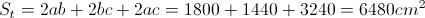 Se vuoi vedere un altro esempio di problema svolto su un prisma retto, vai a questo link.
Se vuoi vedere un altro esempio di problema svolto su un prisma retto, vai a questo link.







