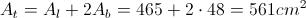Problema svolto sull'area della superficie totale di un prisma retto che ha per base un trapezio isoscele

Risolviamo il seguente problema: Un prisma retto che ha il volume di 720 cm^3, ha per base un trapezio isoscele con la diagonale perpendicolare al lato obliquo. Il rapporto tra la diagonale e l'altezza del trapezio è 5/3 e la somma di questi 2 segmenti è 16 cm. Calcola l'area della superficie totale del prisma. Innanzitutto, l'area della superficie totale del prisma sarà data dalla somma dell'area delle 2 basi, che sono 2 trapezi, con l'area delle facce laterali: , dove At, Al e Ab indicano rispettivamente l'area totale, laterale e di base. Concentriamoci sull'area di base, cioè l'area del trapezio in cui le diagonali sono perpendicolari ai lati obliqui. 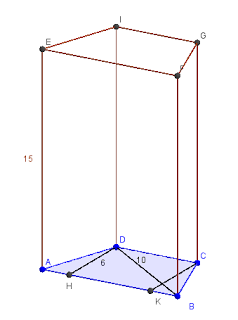Sappiamo che diagonale ed altezza sono l'una i 5/3 dell'altra e la loro somma è pari a 16 cm, perciò la diagonale sarà 5/8 della somma, mentre l'altezza i 3/8 (se usassimo il metodo grafico, rappresenteremmo con 5 unità la diagonale e con 3 l'altezza): 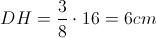Ora del trapezio di base conosciamo la diagonale e l'altezza relativa alle basi. Per il calcolo dell'area abbiamo bisogno delle 2 basi, visto che la relativa formula di calcolo è: 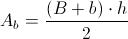Se conosciamo la diagonale e l'altezza, allora del triangolo rettangolo HBD possiamo calcolare la base HB col teorema di Pitagora:
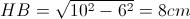
Nel triangolo ABD, rettangolo in D perché diagonale e lato obliquo sono tra loro perpendicolari, HB è proiezione del cateto BD sull'ipotenusa AB. Con il secondo teorema di Euclide possiamo quindi conoscere la lunghezza della base maggiore AB; infatti, secondo tale teorema, ciascun cateto di un triangolo rettangolo è medio proporzionale tra l'ipotenusa e la proiezione del cateto stesso sull'ipotenusa.
Avremo:


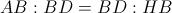
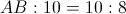
Quindi:

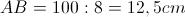
Abbiamo così conosciuto la lunghezza della base maggiore AB. Per ottenere la lunghezza della base minore CD, basta considerare che il trapezio è isoscele, quindi le 2 proiezioni AH e KB devono essere congruenti, e HK = CD. Quindi:

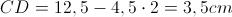
Possiamo calcolare l'area del trapezio, ossia l'area di base Ab del prisma:

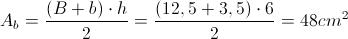
Poiché il volume di un prisma è dato dal prodotto dell'area della superficie di base per l'altezza
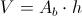, possiamo risalire all'altezza del prisma con la formula inversa: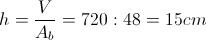

Per l'area della superficie totale basterà sommare 2 volte l'area di base, cioè l'area del trapezio, all'area della superficie laterale Al. Determiniamo quest'ultima, ricordando che:

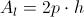
Per calcolare il perimetro 2p, abbiamo bisogno del lato obliquo AD = BC del trapezio, ricavabile attraverso il teorema di Pitagora applicato al triangolo rettangolo AHD:

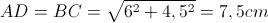
Il perimetro 2p sarà:

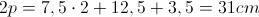
E l'area laterale Al:

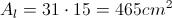
Infine, l'area totale At sarà: