Matematico e magistrato francese, nato a Beaumont-de-Lomagne, 17 agosto 1601 e morto a Castres, 12 gennaio 1665. Pierre de Fermat non svolgeva la professione di matematico a tempo pieno, ma intraprese gli studi di diritto a Tolosa, che lo portarono a lavorare nel parlamento della città come avvocato e, successivamente, come consigliere.
Attratto dalla letteratura classica, studiò anche le opere dei matematici del passato. Dal 1629 si occupò della ricostruzione delle opere classiche pervenute a quel tempo, a partire dai frammenti a disposizione. Ricostruì l’opera Luoghi piani di Apollonio (262 a.C.-190 a.C.), partendo dalle informazioni contenute nella Collezione matematica di Pappo. Durante tale operazione scoprì il principio fondamentale della geometria analitica: «ogniqualvolta in un’equazione finale compaiono due quantità incognite si ha un luogo, l’estremità dell’una descrivendo una linea retta o curva».
Fermat ottenne tale principio applicando gli studi algebrici rinascimentali di Viète (1540-1603) a quelli di Apollonio, di conseguenza è possibile dedurre che il metodo delle coordinate non traeva alcuna origine da problemi di natura pratica.
Grazie alla notazione di Viète, Fermat rappresentò l’equazione lineare espressa dall’enunciato “D in A aequetur B in E”, ovvero, in termini moderni, Dx=By. In tale rappresentazione non fece uso delle ascisse negative. Invece, rappresentò l’equazione lineare ax+by=c2 con un segmento del primo quadrante delimitato dagli assi del sistema di coordinate.
Poiché la sua opera Introduzione ai luoghi comparve solo dopo la sua morte, la geometria analitica sembrò essere una esclusiva invenzione di Descartes (1596-1650), invece il metodo delle coordinate fu scoperto da Fermat prima della pubblicazione dell’opera La géométrie (1637) di Descartes.
La geometria analitica di Fermat era più vicina alla nostra, in quanto utilizzava un sistema di coordinate ortogonali; inoltre il matematico sostenne la possibilità di una geometria analitica di più di due dimensioni, come egli stesso afferma in questo passo: «Vi sono certi problemi che comportano soltanto una incognita, e che possiamo chiamare determinati, per distinguerli dai problemi dei luoghi. Vi sono certi altri problemi che comportano due incognite e che non si possono mai ridurre a una incognita; questi sono i problemi dei luoghi. Nei problemi del primo tipo cerchiamo un unico punto, in quelli del secondo cerchiamo una curva. Ma se il problema che ci viene proposto comporta tre incognite, per soddisfare l’equazione dobbiamo trovare non solo un punto o una curva, ma un’intera superficie. In questo modo hanno origine luoghi superficiali etc.».
Probabilmente la geometria analitica di Fermat era pronta fin dal 1629, anno in cui fece un’importantissima scoperta, descritta più avanti negli anni, in un trattato dal nome Metodo per trovare i massimi e i minimi. Egli determinò un metodo ingegnoso per trovare i massimi e i minimi delle funzioni y=f(x), che corrisponde al nostro procedimento di differenziazione. Per tale ragione è considerato il padre del calcolo differenziale, pur non conoscendo il concetto di limite. Inoltre applicò tale metodo alla determinazione della tangente ad una curva algebrica di equazione y=f(x).
Fermat portò contributi importanti anche nel campo della teoria dei numeri e dell’ottica. Enunciò molti teoremi della teoria dei numeri, ma diede la traccia della dimostrazione solo in un caso. Sono noti i cosiddetti piccolo teorema di Fermat e grande o ultimo teorema di Fermat.
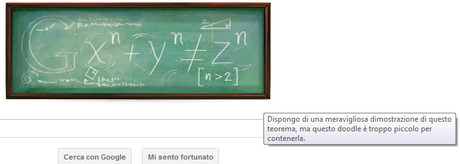
L’ultimo teorema di Fermat (1637) afferma che: «per n>2, non esistono soluzioni intere dell’equazione xn+yn=zn». La dimostrazione di esso non è pervenuta, ma Fermat scrisse ai margini di una copia dell’Arithmetica di Diofanto: «Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina».
La dimostrazione di questo teorema fu cercata da altri matematici nel corso dei secoli, ma solo nel 1994, dopo 7 anni di lavoro sul problema, Andrew Wiles riuscì a darne la dimostrazione. Tale dimostrazione fu premiata il 27 giugno 1997 con il Premio Wolfskehel, consistente in una borsa di 50.000 dollari.
Oggi, per commemorare i 410 anni dalla nascita di Fermat, su Google compare il seguente doodle
e passando sopra l’immagine con il mouse compare la scritta: «dispongo di una meravigliosa dimostrazione di questo teorema, ma questo doodle è troppo piccolo per contenerla».