Legendre e la sua trasformata

Adrien-Marie Legendre fu uno dei più importanti discepoli di Eulero e Lagrange.
È particolarmente noto per alcuni contributi matematici che portano il suo nome, come ipolinomi di Legendre, l'equazione di Legendre e la costante di Legendre.
Tuttavia in questo post focalizzeremo la nostra attenzione sull'importante procedimento matematico noto come trasformata di Legendre.
Cercheremo di presentarla nel modo più semplice e chiaro possibile, ma prima compiremo un breve excursus andando a scoprire la vita di questo straordinario matematico francese.
Legendre nacque a Parigi il 18 settembre 1752.
La sua famiglia era benestante e ciò gli garantì la migliore educazione possibile in fisica e matematica al Collège Mazarin di Parigi.
Nel 1770, all'età di 18 anni, difese la sua tesi al suddetto collegio, ma più che una vera tesi completa come la intendiamo oggi, si trattava di un piano che andava a indicare i futuri studi che avrebbe compiuto e i risultati che si era prefissato di mostrare.
Dal 1775 al 1780 accettò di insegnare all'École Militaire della capitale, assieme a Laplace.
2 anni più tardi spedì un suo saggio di balistica, intitolato Recherches sur la trajectoire des projectiles dans les milieux résistants, all'Accademia di Berlino e vinse un premio.
Aspetto importante dell'evento fu il fatto cheLagrange (allora direttore della sezione fisico-matematica dell'Accademia di Berlino) notò tale saggio e chiese maggiori informazioni sul giovane autore del saggio a Laplace, il quale rispose tessendone grandi elogi.
Sempre nel 1782, in qualità di successore dello stesso Laplace (promosso membro associato), Legendre venne nominato "aggiunto" ("adjoint mécanicien") presso l'Accademia di Parigi.
Egli stesso, successivamente, nel 1785, venne a sua volta promosso.
In questi anni Legendre pubblicò lavori in svariate aree della matematica.
Nello specifico, si interessò di:

• meccanica celeste, nell'articolo Recherches sur la figure des planètes datato 1784, il quale contiene per giunta i polinomi di Legendre;
• teoria dei numeri, nell'articolo Recherches d'analyse indéterminée del 1785;
• teoria delle funzioni ellittiche, pubblicando articoli, nel 1786, sull'integrazione degli archi ellittici.

L'Accademia parigina venne abolita nel 1793 e ricostituita come parte dell'Institut de France.
Quell'anno Legendre convolò a nozze con Marguerite-Claudine Couhin, che l'aiutò a rimettere gli affari in ordine.
Il matematico, come avrebbe in seguito scritto a Jacobi, ebbe infatti gravi problemi economici durante il travagliato periodo della Rivoluzione Francese e dunque accettò vari incarichi.
Nel 1787 era stato membro di un comitato accademico di geodesia, i cui impegni l'avevano condotto a Londra, ove nel 1789 sarebbe stato nominato membro della prestigiosa Royal Society.
Nel 1791, e dal 1794 in poi, fece parte di varie commissioni che arrivarono infine a stabilire il sistema metrico decimale.
Sempre nel 1794 il matematico pubblicò Eléments de géométrie, il testo elementare più importante sull'argomento per circa un secolo.
Questo libro, infatti, riassume e semplifica in modo straordinario le proposizioni degli Elementi di Euclide, per creare un'opera che si confacesse di più a un libro di testo.
L'anno successivo Legendre divenne uno dei 6 membri della sezione matematica dell'Accademia delle Scienze, rifondata come Istituto Nazionale delle Scienze e delle Arti.
Nel 1803 Napoleone diede una nuova organizzazione all'Istituto e Legendre divenne un membro della sezione di geometria.
Tra il 1799 e il 1815 ricoprì inoltre il ruolo di esaminatore presso l'École Militaire.
Nel 1813, inoltre, prese il posto di Lagrange al Bureau des Longitudes, posto che conservò fino alla morte.
Nel 1824 Legendre si era rifiutato di votare per il candidato del governo per l'Istituto Nazionale, gesto che lo portò a perdere la sua pensione e morire in povertà il 10 gennaio 1833, a Parigi, città natale.
È giunto il momento di parlare della trasformata di Legendre!

La trasformata (o trasformazione di Legendre) è un particolare algoritmo matematico che trasforma una funzione convessa a valori reali di variabile reale in un'altra funzione convessa, dipendente esplicitamente dalla derivata della funzione di partenza.
Detta così, pochi ci avranno capito qualcosa.
Cerchiamo di chiarire la questione.
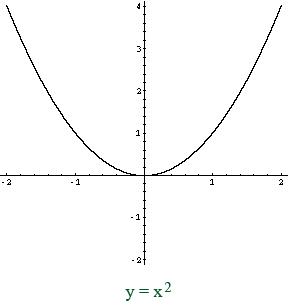
Prendiamo una funzione y = f(x) convessa.
Che significa convessa?
Semplicemente che la derivata seconda di quella funzione, calcolata in x, sarà maggiore di 0.
In simboli:

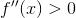
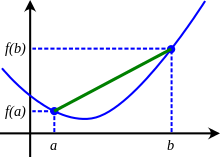
In termini geometrici questo si traduce nel fatto che presi 2 punti del grafico della funzione convessa, il segmento che li unisce si trova al di sopra della funzione, come ben illustra la seguente immagine:

Giusto per completezza, questo sarebbe il grafico di una generica funzione concava, l'opposto della funzione convessa:

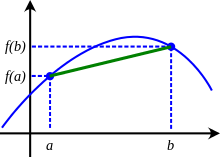
Definiamo trasformata di Legendre della funzione f considerata una nuova funzione, che indichiamo con g, di una nuova variabile p.
Come si costruisce questa trasformata?
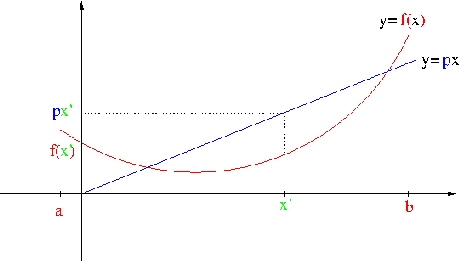
Innanzitutto si traccia sul piano cartesiano Oxy il grafico della funzione di partenza f.
Dopodiché consideriamo un numero p e la relativa retta passante per l'origine degli assi:

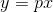
Prendiamo ora il punto x = x(p) nel quale la distanza fra la curva e la retta lungo la verticale risulta massima (in figura corrisponde al punto x').

Pertanto la funzione

che possiamo indicare più sinteticamente come:

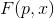
presenta un massimo in x, per p fissato, proprio nel punto x( p) [in figura viene sempre indicato con x'].
Costruiamo allora la nuova funzione g(p), la trasformata di Legendre, come

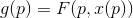
La coordinata p la conosciamo, avendola fissata arbitraria; ciò che va determinato è invece il punto di massimo x( p).
Come si fa?
Semplice, essendo un punto di massimo (se vi ricordate il teorema di Fermat), esso è un punto in cui la derivata della funzione F rispetto a x sarà nulla.
In simboli:

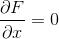
Siccome abbiamo stabilito che:

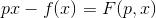
derivando tale espressione rispetto a x si ottiene:

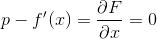
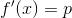
Visto che f è una funzione convessa, il punto x(p), se esiste, è univocamente determinato.
Osserviamo un paio di esempi inerenti alla trasformata di Legendre.
Consideriamo la funzione convessa

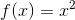
una parabola rivolta verso l'alto, con vertice nell'origine degli assi, insomma!

Allora senza dubbio possiamo dire che

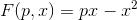
Inoltre, siccome abbiamo affermato che

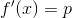
in questo caso abbiamo:

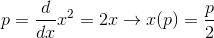
Abbiamo dunque derivato la funzione di partenza e individuato il punto di massimo x( p).
A questo punto, per ottenere la nuova funzione (cioè la trasformata), è sufficiente andare a sostituire alla x nell'espressione

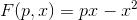
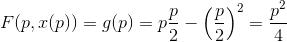
Consideriamo ora un'altra parabola, leggermente più complessa:

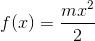
e ripetiamo il procedimento per determinare la trasformata.
Innanzitutto è facile stabilire che:

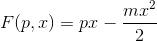
Deriviamo ora l'espressione di partenza rispetto a x e poniamo questa derivata uguale a p:

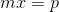
da cui:

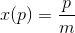
A questo punto, per ottenere la trasformata, andiamo a sostituire alla x nell'espressione

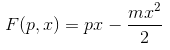
il valore x( p) ricavato.
Ne consegue che la trasformata di Legendre è equivalente a:

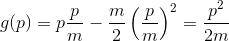
Una particolare proprietà della trasformata di Legendre è il fatto che essa è involutiva, ovvero il suo quadrato è la trasformazione identica: se infatti la funzione f va in g sotto la trasformazione di Legendre, allora trasformando a sua volta g si otterrà nuovamente f .
Magico no?
Un'ultimissima lecita domanda: a cosa diavolo serve la trasformata di Legendre?
Senza entrare nei dettagli (troppo complessi per essere affrontati in un singolo post), concludiamo dicendo che essa trova fondamentali applicazioni sia nell'ambito della meccanica analitica (la trasformazione che fa passare da una funzione lagrangiana ad una funzione hamiltoniana è infatti un caso particolare di trasformata di Legendre) che in quello della termodinamica.