Piramide con base romboidale, problema risolto

Una nostra lettrice ci chiede aiuto nel risolvere questo problema di geometria solida, programma di terza media.

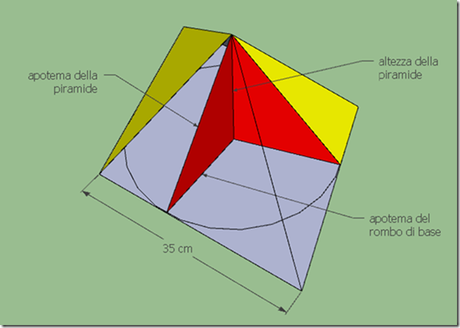
Problema: Una piramide retta ha per base un rombo, in cui la diagonale minore è 3/4 della maggiore e la loro differenza è di 14 cm. Lo spigolo della piramide forma con la diagonale minore un angolo di 45 gradi. Determina il volume della piramide e la sua area totale.

Soluzione: Conosciamo il rapporto e la differenza delle diagonali, allora usiamo la proprietà dello scomporre applicata alla proporzione:

diagonale magg. : diagonale min. = 4 : 3

Proprietà dello scomporre: (diag. magg. – diag. min.) : diag. min. = (4 – 3) : 3

14 : diag. min. = 1 : 3  

risolvo:

diagonale minore = 14 x 3 : 1 = 42 cm

diagonale maggiore = diagonale minore + 14 = 42 + 14 = 56 cm

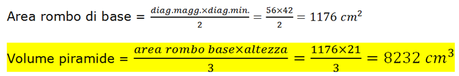
Poiché lo spigolo forma 45° con la diagonale minore, l’altezza della piramide è uguale alla metà della diagonale minore: 42 : 2 = 21 cm

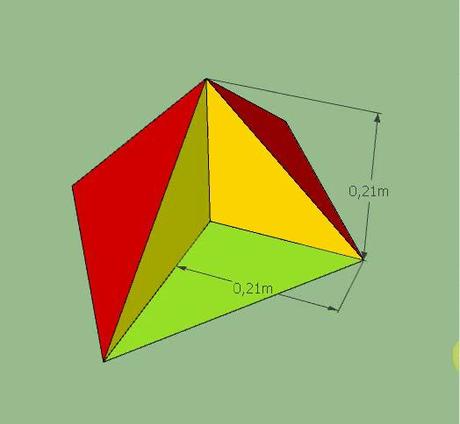
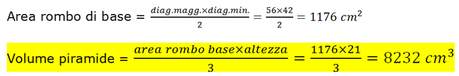
Per trovare l’area totale ci manca quella laterale che sappiamo si calcola con la formula: perimetro per apotema diviso due.

Cominciamo a trovare la misura del lato del rombo, con Pitagora.

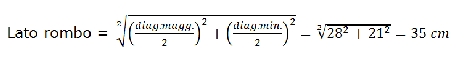
Perimetro del rombo = lato x 4 = 35 x 4 = 140 cm

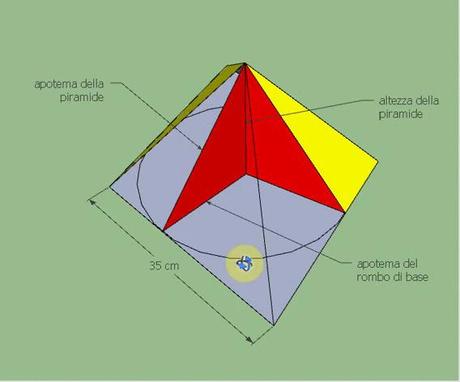
Per calcolare l’apotema della piramide osserviamo queste immagini: