Problema svolto: determinare le coordinate di un punto che divide un segmento in 2 parti proporzionali secondo un dato rapporto

Risolviamo il seguente problema di geometria analitica:Nel segmento di estremi A(-2;9) e B(14;1) determina le coordinate dei punti che lo dividono in due parti proporzionali ai numeri 5 e 3.Se il segmento viene diviso in due parti proporzionali ai numeri 5 e 3, possiamo dire più semplicemente che uno dei due segmenti in cui viene diviso il segmento AB sarà i 5/3 dell'altro. 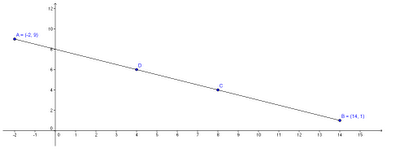In particolare, dobbiamo determinare le coordinate di 2 punti C e D, in quanto sono possibili due situazioni (vedi fig.): 1) C divide il segmento AB in maniera tale che AC sia i 5/3 di CB;2) D divide il segmento AB in maniera tale che AD sia i 3/5 di DB.1) Consideriamo il primo caso:Siccome AC = 5/3 CB, quest'ultima equazione dovrà essere valida anche per la distanza tra le ascisse di questi due segmenti e per la distanza tra le ordinate. Notiamo infatti che la retta su cui giace AB e l'asse delle ascisse formano due trasversali che tagliano il fascio di rette parallele condotto perpendicolarmente all'asse delle ascisse (tali rette sono tratteggiate in figura).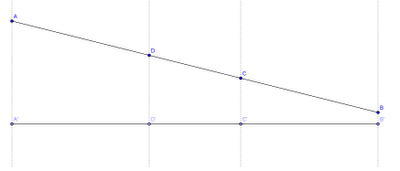

Per il teorema di Talete, a segmenti proporzionali su una trasversale corrispondono segmenti proporzionali sull'altra trasversale, per cui in parole semplici il rapporto tra i segmenti AC e CB dev'essere lo stesso di quello tra i segmenti A'C' e C'B'. Analogo ragionamento si può seguire per le ordinate. Quindi dovrà essere:




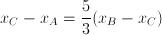
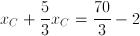
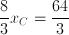
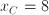
Analogamente possiamo trovare l'ordinata del punto C (saltando qualche passaggio):


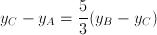
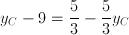
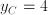
Il punto C avrà coordinate C(8;4).2) Ragioniamo in maniera analoga per il punto D, che divide AB in modo tale che AD sia lungo 3/5 di DB e avremo:





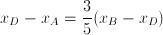
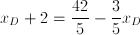
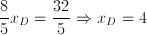
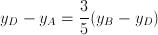
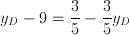
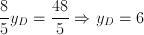
Il punto D ha coordinate D(4;6).